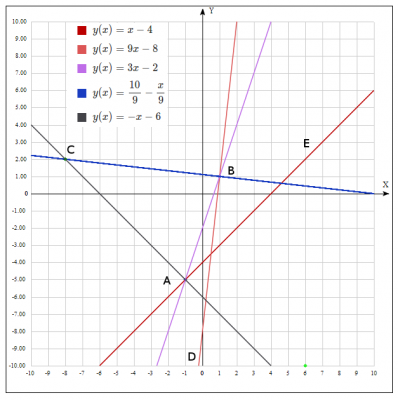
Задано: Дано координати \(А (А_х ;А_у)\) та \(В(В_х ;В_у)\) вершин трикутника АВС, рівняння двох його висот \(х-у+m=0\) і \(9x-y+n=0\) та координати довільної точки \(Р(Р_х; Р_у)\)
Координати \(А (А_х ;А_у)= (-1;-5)\) , Координати \(В(В_х ;В_у)=(1;1)\), Координати \(Р(Р_х; Р_у)=(6;-10)\), \(m=-4, n=-8\)
Знайти : рівняння сторін трикутника АВС
Розв'язання:
1) Рівняння сторони АВ
Рівняння сторони будемо шукати за допомогою формули рівняння прямої, що проходить через дві задані точки \( \frac{x-x_1}{x_2-x_1} = \frac{y-y_1}{y_2-y_1} \quad (1) \)
Підставляємо координати вершин:
рівняння сторони \( AB \), при відомих координатах вершини \( А(-1;-5); В(1;1)\) $$ AB \quad \frac{x+1}{1+1} = \frac{y+5}{1+5} => y =3x - 2$$
Відповідь: рівняння сторони \(AB\): \( y =3x - 2 \quad (2)\)
2) Рівняння сторони ВC
У завданні дано координати точки \(В (1; 1) \), координата точки \(C \) не відома, але є рівняння висот, опущених з точок \(A \) і \(B \). Визначимо, яка з висот проходить через точку \(B \). Підставимо координати точки \(B \) в рівняння висот, якщо висота проходить через цю точку, то після підстановки координат в рівняння висоти ми отримаємо рівність. $$ В(1; 1) \quad х-у-4 = 0 => 1-1 -4 \ne 0 $$$$ В (1; 1) \quad 9x-y-8 = 0 => 9- 1 - 8 = 0 $$ Рівняння висоти \(BF \), що проходить через точку $$ В(1; 1) \quad 9x-y-8 = 0 => y = 9x-8 \quad (3) $$ Скористаємося властивістю кутового коефіцієнта перпендикулярних прямих: \(k_1 = - \frac {1}{k_2} \).
Знайдемо кутовий коефіцієнт прямої сторони \(BC\) з рівняння (3). Отримаємо $$k_ {BF} = 9 => k_ {BC} = - \frac {1}{BF} = - \frac{1}{9} $$
Знайдемо рівняння прямої \(BC \), для цього скористаємося формулою рівняння прямої що проходить через задану точку \(B (1; 1) \) в заданому напрямку \(k_ {BC} = - \frac {1}{9} \) $$ y - y_0 = k (x - x_0) \quad (4) $$ Отримаємо $$ y - 1 = - \frac {1}{9}(x - 1) => y = \frac{10}{9} - \frac{1}{9}x $$
Відповідь: рівняння сторони \(BC\): \( y = \frac{10}{9} - \frac{1}{ 9}x \quad (5)\)
3) Рівняння сторони AC
У завданні дано координати точки \(A (-1; 5) \), координата точки \(C \) не відома, але є рівняння висот, опущених з точок \(A \) і \(B \). Рівняння висоти яка проходить через точку \(A \) $$ A(-1; -5) \quad х-у-4 = 0 => -1+5 - 4 = 0 $$ Рівняння висоти \(AE \), що проходить через точку $$ A(-1; -5) \quad х-у-4 = 0 => y = x - 4 \quad (6) $$ Скористаємося властивістю кутового коефіцієнта перпендикулярних прямих: \(k_1 = - \frac {1}{k_2} \).
Знайдемо кутовий коефіцієнт прямої сторони \(AC\) з рівняння (6). Отримаємо $$k_ {AE} = 1 => k_ {AC} = - \frac {1}{AE} = - 1 $$
Знайдемо рівняння прямої \(AC \), для цього скористаємося формулою рівняння прямої що проходить через задану точку \(A (-1; -5) \) в заданому напрямку \(k_ {AC} = - 1\) (4) $$ y - y_0 = k (x - x_0) $$ Отримаємо $$ y +5 = - (x + 1) => y = -x - 6 $$
Відповідь: рівняння сторони \(AC\): \( y = -x - 6 \quad (7)\)
4) Координати вершини \(C\)
Координати вершини \(C \) знайдемо як точку перетину двох прямих \(AC \) і \(BC \) для цього складемо систему рівнянь і вирішимо її $$ \begin{cases} y = -x - 6 \\ y = \frac{10}{9} - \frac{1}{9} x \end{cases} => \begin{cases} y = -x - 6 \\ 9y = 10 - x \end{cases} => \begin{cases} y = -x - 6 \\ 8y = 16 \end{cases} => \begin{cases} x = -8 \\ y = 2 \end{cases} $$
Відповідь: координати вершини \(C(-8;2)\)