В задаче необходимо найти прямоугольник наибольшей площади. Нахождение наибольшего и наименьшего значения функции означает нахождение экстремума функции от одного переменного. В нашем случае функцией является площадь прямоугольника, а переменной - значение одной из сторон. Однако площадь прямоугольника равна \(S = a*b\), т.е. площадь зависит от двух переменных - сторон \( a,b\), т.е. необходимо найти зависимость между \( a,b\), подставить в формулу площади и мы получим зависимость площади от одной из сторон прямоугольника. Формулу зависимости между \( a,b\) мы можем найти на основании условия задачи. Цель решения задачи ясна, приступаем к ее решению.
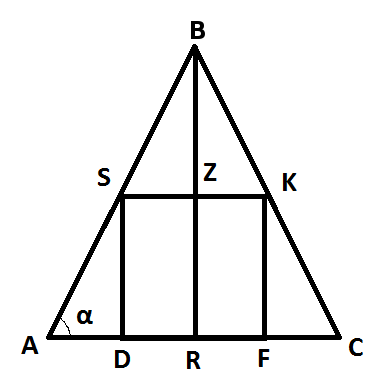
Рассмотрим равнобедренный треугольник \( ΔABC\), допусти что прямоугольник \( DSKF\) - искомый прямоугольник наибольшей площади. Высота \(h = BR = 4 cm\). Для начала найдем стороны треугольника. Известно, что треугольник равнобедренный и его периметр равен 16, запишем это \( AB=BC\), \( AB+BC+CD = 16 =>2*AB+ AC = 16\). Для прямоугольного треугольника \( ΔABR \) запишем теорему Пифагора \( BR^2 + (\frac{AC}{2})^2 = AB^2 => 4^2 + (\frac{AC}{2})^2 = AB^2 \). Составим систему уравнений $$\begin{cases} 2*AB+ AC = 16 \\ 4^2 + (\frac{AC}{2})^2 = AB^2\end{cases} =>\begin{cases} AB = 8 - \frac{AC}{2} \\ 16 + \frac{AC^2}{4} = 64 - 8AC + \frac{AC^2}{4}\end{cases} =>$$$$\begin{cases} AB = 8 - \frac{AC}{2} \\ AC = 6 \end{cases} =>\begin{cases} AB = 5 \\ AC = 6 \end{cases} $$нашли стороны треугольника. Теперь возвращаемся к основной задаче - поиск сторон прямоугольника. Рассмотрим два треугольника \( ΔABR\) и \( ΔASD\) это два подобных треугольника по двум углам. Обозначим \( DS = x, DF = y\). Составим пропорцию $$ \frac{DS}{BR} = \frac{AD}{AR} =>\frac{x}{h} = \frac{\frac{AC-DF}{2}}{\frac{AC}{2}} =>$$$$ \frac{x}{4} = \frac{6-y}{6} => x = 4-\frac{2}{3}y $$Получили искомую зависимость между сторонами. Теперь подставим в формулу площади прямоугольника, имея функцию зависимости площади от одной переменной найдем экстремум функции, т.е. первую производную и приравняем ее к 0. $$S = x*y = (4-\frac{2}{3}y) *y = 4y - \frac{2}{3}*y^2$$$$S' = (4y - \frac{2}{3}*y^2) = 4- \frac{4}{3}y = 0 => y = 3$$ подставим в формулу для \( x = 4-\frac{2}{3}y = 2\). Получили длины сторон прямоугольника \( x = 2, y=3\) при которых площадь будет наибольшей. Обращаю внимание, что при поиске экстремума было использовано необходимое условие существования экстремума - первая производная равна 0, достаточное условие я не проверял, т.к. полученная формула площади \( S = 4y - \frac{2}{3}*y^2\) парабола, а так как при \( y^2\) стоит отрицательный коэффициент, то это означает, что ее оси направлены вниз, т.е. полученный экстремум - точка максимума.
Ответ: длины сторон равны прямоугольника, наибольшей площади равны \(2 cm\) и \(3 cm\)



