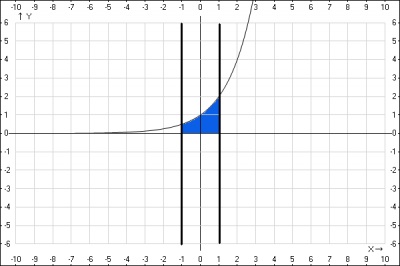
Решение: при вращении криволинейной трапеции вокруг оси Ox, которая ограничена сверху прямой \( y=2^x \), а справа и слева прямыми \(x=-1\) и \(x=1\) и снизу прямой \(y =0\), образуется тело вращения - обрезанный конус.
Находим объем фигуры вращения.
Рассчитаем объем фигуры вращения вокруг оси Ox - обрезанного конуса, по формуле $$V_x = \pi \int_a^b y^2dx$$ где \(a = -1\), \(b=1\), \( y = 2^x \). Подставляем данные в формулу $$V_x = \pi \int_{-1}^1 2^{2x}dx = \pi \frac{2^{2x}}{2\ln(2)}|_{-1}^1 = $$$$ = \frac{\pi}{2\ln(2)}[2^{2*1} - 2^{2*(-1)}] = \frac{15\pi}{8\ln(2)} $$
Ответ: объем фигуры вращения равен \(V_x = \frac{15\pi}{8\ln(2)} \)