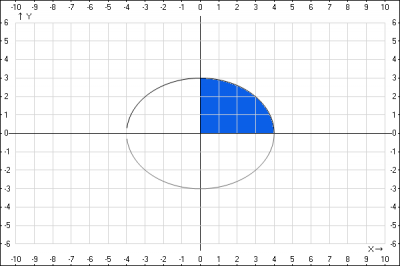
–†–µ—И–µ–љ–Є–µ: —А–∞—Б—Б–Љ–Њ—В—А–Є–Љ —А–Є—Б—Г–љ–Њ–Ї. –Ш–Ј —А–Є—Б—Г–љ–Ї–∞ –≤–Є–і–љ–Њ, —З—В–Њ –Є—Б–Ї–Њ–Љ–∞—П —Д–Є–≥—Г—А–∞ –Њ–≥—А–∞–љ–Є—З–µ–љ–љ–∞—П –ї–Є–љ–Є—П–Љ–Є —Б–≤–µ—А—Е—Г \( \frac{x^{2}}{16}+\frac{y^{2}}{9}=1 \) —Б–ї–µ–≤–∞ \(y=0\) —Б–љ–Є–Ј—Г \(x=0\), —В.–µ –љ–∞–Љ –љ—Г–ґ–љ–Њ –љ–∞–є—В–Є –њ–ї–Њ—Й–∞–і—М —Н–ї–ї–Є–њ—Б–∞ –≤ –њ–µ—А–≤–Њ–є —З–µ—В–≤–µ—А—В–Є. –Ф–ї–Є–љ–∞ –±–Њ–ї—М—И–Њ–є –њ–Њ–ї—Г–Њ—Б–Є —А–∞–≤–љ–∞ \(a^2 = 16 => a=4\). –Я—А–µ–Њ–±—А–∞–Ј—Г–µ–Љ —Г—А–∞–≤–љ–µ–љ–Є–µ —Н–ї–ї–Є–њ—Б–∞ —Б —Г—З–µ—В–Њ–Љ —В–Њ–≥–Њ,—З—В–Њ –≤ –њ–µ—А–≤–Њ–є —З–µ—В–≤–µ—А—В–Є \(x > 0, \quad y > 0\), –њ–Њ–ї—Г—З–∞–µ–Љ $$ \frac{x^{2}}{16}+\frac{y^{2}}{9}=1 => y = 3\sqrt{1- \frac{x^2}{16}}$$ –њ–Њ–ї—Г—З–Є–ї–Є —П–≤–љ–Њ –≤—Л—А–∞–ґ–µ–љ–љ—Г—О —Д—Г–љ–Ї—Ж–Є—О \(y = f(x)\). –Э–∞—Е–Њ–і–Є–Љ –њ–ї–Њ—Й–∞–і—М —Д–Є–≥—Г—А—Л $$S = \int_0^43\sqrt{1- \frac{x^2}{16}}dx = \quad (1)$$
1. –Э–∞–є–і–µ–Љ –љ–µ–Њ–њ—А–µ–і–µ–ї–µ–љ–љ—Л–є –Є–љ—В–µ–≥—А–∞–ї \( \int \sqrt{1- \frac{x^2}{16}}dx \)–Я—А–Є–Љ–µ–љ–Є–Љ —Д–Њ—А–Љ—Г–ї–∞ –Є–љ—В–µ–≥—А–Є—А–Њ–≤–∞–љ–Є—П –њ–Њ —З–∞—Б—В—П–Љ \( \int udv = uv - \int vdu\). –Т–≤–µ–і–µ–Љ –Њ–±–Њ–Ј–љ–∞—З–µ–љ–Є—П \(dv = dx => v = x\), –∞ \(u = \sqrt{1- \frac{x^2}{16}} => du = -\frac{x}{16\sqrt{1- \frac{x^2}{16}}}dx \), –њ–Њ–і—Б—В–∞–≤–ї—П–µ–Љ $$ \int \sqrt{1- \frac{x^2}{16}}dx = x \sqrt{1- \frac{x^2}{16}} + \int x* \frac{x}{16\sqrt{1- \frac{x^2}{16}}}dx =$$
–≤—Л–і–µ–ї–Є–Љ —Ж–µ–ї—Г—О —З–∞—Б—В—М –≤ –і—А–Њ–±–Є –Є–љ—В–µ–≥—А–∞–ї–∞ $$ = x \sqrt{1- \frac{x^2}{16}} - \int \frac{1 - \frac{x^2}{16} - 1}{\sqrt{1- \frac{x^2}{16}}}dx = x \sqrt{1- \frac{x^2}{16}} - \int \sqrt{1- \frac{x^2}{16}}dx + \int \frac{1}{\sqrt{1- \frac{x^2}{16}}}dx = $$ –њ—А–Є–Љ–µ–љ–Є–Љ —Д–Њ—А–Љ—Г–ї—Г —В–∞–±–ї–Є—З–љ–Њ–≥–Њ –Є–љ—В–µ–≥—А–∞–ї–∞ –∞—А–Ї—Б–Є–љ—Г—Б–∞ \( \int \frac{1}{ \sqrt{1-(ax)^2}} = \frac{1}{a}\arcsin(ax)\), –њ–Њ–ї—Г—З–∞–µ–Љ $$ \int \sqrt{1- \frac{x^2}{16}}dx = x \sqrt{1- \frac{x^2}{16}} - \int \sqrt{1- \frac{x^2}{16}}dx + 4\arcsin(\frac{x}{4}) =>$$ —Б–њ—А–∞–≤–∞ –Є —Б–ї–µ–≤–∞ –њ–Њ–ї—Г—З–Є–ї–Є —А–∞–≤–љ—Л–µ –Є–љ—В–µ–≥—А–∞–ї—Л, –њ–µ—А–µ–љ–µ—Б–µ–Љ –Є—Е –≤ –ї–µ–≤—Г—О —З–∞—Б—В—М —А–∞–≤–µ–љ—Б—В–≤–∞ $$ 2 \int \sqrt{1- \frac{x^2}{16}}dx = x \sqrt{1- \frac{x^2}{16}} + 4\arcsin(\frac{x}{4}) => $$$$ \int \sqrt{1- \frac{x^2}{16}}dx = \frac{1}{2}x \sqrt{1- \frac{x^2}{16}} + 2\arcsin(\frac{x}{4})$$
2. –њ–Њ–і—Б—В–∞–≤–ї—П–µ–Љ —А–µ–Ј—Г–ї—М—В–∞—В–∞ –≤ (1) $$ S = 3\int_0^4\sqrt{1- \frac{x^2}{16}}dx = 3(\frac{1}{2}x \sqrt{1- \frac{x^2}{16}} + 2\arcsin(\frac{x}{4}))|_0^4 = $$ –њ—А–Є–Љ–µ–љ–Є–Љ —Д–Њ—А–Љ—Г–ї—Г –Э—М—О—В–Њ–љ–∞ - –Ы–µ–є–±–љ–Є—Ж–∞ \(\int_a^bf(x)dx = F(b) - F(a)\), –њ–Њ–ї—Г—З–∞–µ–Љ $$ = 3(\frac{1}{2}*4 \sqrt{1- \frac{4^2}{16}} + 2\arcsin(\frac{4}{4}) - \frac{1}{2}0 \sqrt{1- \frac{0^2}{16}} 0 2\arcsin(\frac{0}{4})) =3\pi $$
–Ю—В–≤–µ—В: –њ–ї–Њ—Й–∞–і—М —Д–Є–≥—Г—А—Л, –Њ–≥—А–∞–љ–Є—З–µ–љ–љ–∞—П –Ј–∞–і–∞–љ–љ—Л–Љ–Є –ї–Є–љ–Є—П–Љ–Є —Б–≤–µ—А—Е—Г \( \frac{x^{2}}{16}+\frac{y^{2}}{9}=1 \) —Б–ї–µ–≤–∞ \(y=0\) —Б–љ–Є–Ј—Г \(x=0\) —А–∞–≤–љ–∞ \(S = 3\pi \)