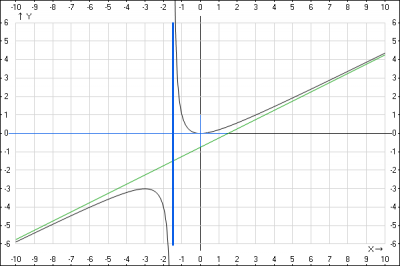
Исследуем функцию \( y= \frac{x^2}{2x+3} \) и построим ее график.
1. Область определения.
Областью определения рациональной функции (дробь): знаменатель не равен нулю, т.е. \(2x -3 \ne 0 => x \ne -\frac{3}{2} \). ОДЗ $$D_f=(-\infty; -\frac{3}{2}) \cup ( -\frac{3}{2} ;+\infty)$$
2. Точки разрыва функции и их классификация.
Функция имеет одну точку разрыва \(x = -\frac{3}{2} \)
исследуем точку \( x= -\frac{3}{2} \). Найдем предел функции справа и слева от точки разрыва, справа $$ \lim_{x \to -\frac{3}{2}+0} \frac{x^2}{2x+3} = + \infty $$ и слева от точки $$ \lim_{x \to -\frac{3}{2}-0} \frac{x^2}{2x+3} = - \infty $$ Это точка разрыва второго рода т.к. односторонние пределы равны \( \infty\).
Прямая \(x = -\frac{3}{2} \) является вертикальной асимптотой.
3. Четность функции.
Проверяем на четность \(f(-x) = \frac{(-x)^2}{-2x+3} \) функция является ни четной, ни не четной.
4. Нули функции (точки пересечения с осью Ox). Интервалы знакопостоянства функции.
Нули функции (точка пересечения с осью Ox): приравняем \(y=0\), получим \( \frac{x^2}{2x+3} = 0 =>x = 0 \). Кривая имеет одну точку пересечения с осью Ox в точке с координатами (0;0).
Интервалы знакопостоянства функции. Кривая имеет одну точку пересечения с осью Ox это x =0 и одну точку разрыва \(x = -\frac{3}{2} \), т.е. три интервала знакопостоянства
Определим знак функции на этих интервалах
интервал \((-\infty; -\frac{3}{2}) \) найдем значение функции в любой точке \(f(-2) = \frac{(-2)^2}{2(-2)+3} < 0 \), на этом интервале функция отрицательная \(f(x) < 0 \), т.е. функция находится ниже оси Ox
интервал \(( -\frac{3}{2}; 0) \) найдем значение функции в любой точке \(f(-1) = \frac{(-1)^2}{2(-1)+3} > 0 \), на этом интервале функция положительная \(f(x) > 0 \), т.е. функция находится выше оси Ox
интервал \((2; +\infty) \) найдем значение функции в любой точке \(f(3) = \frac{(2)^2}{2*2+3} > 0 \), на этом интервале функция положительная \(f(x) > 0 \), т.е. функция находится выше оси Ox
5. Точки пересечения с осью Oy: для этого нужно приравнять \(f(0) = \frac{0^2}{2*0+3} = 0 \). Кривая имеет одну точку пересечения с осью Oy в точке с координатами \((0; 0)\).
6. Интервалы монотонности. Экстремумы функции.
Найдем критические (стационарные) точки, для этого найдем первую производную и приравняем ее к нулю $$y' = ( \frac{x^2}{2x+3} )'= \frac{2x(2x+3) - 2x^2}{(2x+3)^2}= $$$$ = \frac{4x^2+6x - 2x^2}{(2x+3)^2} = \frac{2x(x+3)}{(2x+3)^2}$$ приравняем к 0 $$ \frac{2x(x+3)}{(2x+3)^2} =0 => x_1= 0; \quad x_2 = -3 $$ функция имеет две критические (стационарные) точки.
Найдем значение функции в этих точках
\(f(-3)= \frac{(-3)^2}{2(-3)+3} = -3 \), получили координаты критической точки \((-3; -3)\)
\(f(0)= \frac{0^2}{2-0+3} = 0 \), получили координаты критической точки \((0; 0)\)
Интервалы монотонности.
Функция имеет две критические точки и одну точку \(x=-\frac{3}{2}\), в которых производная не определена (ОДЗ), они делят ось Ox на четыре интервала монотонности.
интервал \((-\infty; -3)\) найдем знак первой производной в любой точке интервала \( f(-4) = \frac{2(-4)(-4+3)}{(2(-4)+3)^2} > 0\), на этом интервале функция возрастает.
интервал \(( -3; -\frac{3}{2})\) найдем знак первой производной в любой точке интервала \(f(-2) = \frac{2(-2)(-2+3)}{(2(-2)+3)^2} < 0\), на этом интервале функция убывает.
интервал \(( -\frac{3}{2}; 0)\) найдем знак первой производной в любой точке интервала \(f(-1) = \frac{2(-1)(-1+3)}{(2(-1)+3)^2} < 0\), на этом интервале функция убывает.
интервал \((0; +\infty)\) найдем знак первой производной в любой точке интервала \(f(1) = \frac{2*1(1+3)}{(2*1+3)^2} > 0\), на этом интервале функция возрастает.
Достаточным условием существования экстремума является изменение знака производной при переходе через критическую точку.
Для критической точки получаем:
\(x = -3\): \(\quad + \quad 0 \quad -\), т.е. функция имеет точку максимума с координатами \((-3; -3)\)
\(x = 0\): \(\quad - \quad 0 \quad +\), т.е. функция имеет точку минимума с координатами \((0; 0)\)
7. Интервалы выпуклости и вогнутости. Точки перегиба.
Для нахождения интервалов выпуклости и вогнутости найдем вторую производную функции и приравняем ее к нулю $$y'' = ( \frac{2x(x+3)}{(2x+3)^2})'= (\frac{2x^2+6x}{(2x+3)^2})' = $$$$ = \frac{(4x+6)(2x+3)^2 -4(2x^2+6x)(2x+3)}{(2x+3)^4} = 2\frac{4x^2+12x+9 -4x^2-12x}{(2x+3)^3} = $$$$ = \frac{18}{(2x+3)^3}$$ Приравняем к нулю $$ \frac{18}{(2x+3)^3} = 0 => $$ точек возможного перегиба функция не имеет. Рассмотрим выпуклость функции на ОДЗ
интервал \((-\infty; -\frac{3}{2})\) найдем знак второй производной в любой точке \(f''(-2) = \frac{18}{(2(-2)+3)^3} < 0 \), на этом интервале вторая производная функции отрицательная \(f''(x) < 0 \) - функция выпуклая вверх (вогнутая).
интервал \(( -\frac{3}{2}; + \infty )\) найдем значение второй производной в любой точке \(f''(0) = \frac{18}{(2*0+3)^3} > 0\), т.е. на этом интервале вторая производная функции положительная \(f''(x) > 0 \) - функция выпуклая вниз (выпуклая).
Точки перегиба.
Функция точек перегиба не имеет.
8. Асимптоты.
Вертикальная асимптота. График функции имеет вертикальные асимптоты x =1 (см. п.2).
Наклонная асимптота.
Для того, чтобы график функции \(у= \frac{x^2}{2x+3} \) при \(x \to \infty\) имел наклонную асимптота \(y = kx+b\), необходимо и достаточно, чтобы существовали два предела $$\lim_{x \to +\infty}=\frac{f(x)}{x} =k $$находим его $$ \lim_{x \to +\infty} \frac{x^2}{x(2x+3)} = \frac{1}{2} => k= \frac{1}{2}$$ и второй предел $$ \lim_{x \to +\infty}(f(x) - kx) = b$$ подставляем $$ \lim_{x \to +\infty}( \frac{x^2}{2x+3} - \frac{x}{2}) = \lim_{x \to +\infty}( \frac{2x^2 - 2x^2-3x}{2(2x+3)} ) = -\frac{3}{4}$$
Уравнение наклонной асимптоты \( y = \frac{x}{2} - \frac{3}{4}\)
Горизонтальная асимптота: для того, чтобы существовала горизонтальная асимптота, необходимо, чтобы существовал предел $$\lim_{x \to +\infty}f(x) = b$$ найдем его $$ \lim_{x \to +\infty} \frac{x^2}{2x+3}= \infty $$
Горизонтальной асимптоты нет.
Определим, с какой стороны приближается график функции к наклонной асимптоте, для этого найдем пределы:
$$ \lim_{x \to +\infty} ( \frac{x^2}{2x+3} - ( \frac{x}{2} - \frac{3}{4})) = \lim_{x \to +\infty} \frac{9}{4(2x+3)} = +0 $$ график функции приближается к асимптоте сверху
$$ \lim_{x \to -\infty} ( \frac{x^2}{2x+3} - ( \frac{x}{2} - \frac{3}{4})) = \lim_{x \to -\infty} \frac{9}{4(2x+3)} = -0 $$ график функции приближается к асимптоте снизу
9. График функции.