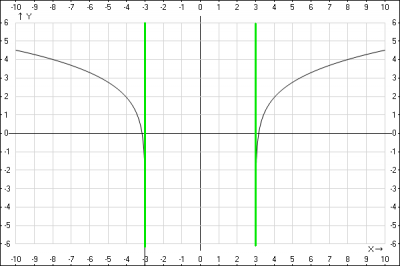
Исследуем функцию \( y= \ln(x^2-9) \) и построим ее график.
1. Область определения.
Областью определения функции будет область определения логарифма, т.е. \(x^2-9 > 0 => \) \(D_f= (-\infty; -3) \cup (3;+\infty)\)
2. Точки разрыва функции и их классификация.
Функция на ОДЗ точек разрыва не имеет.
3. Четность функции.
Проверяем на четность \(f(-x) = \ln((-x)^2-9) = \ln(x^2-9) \) функция является четной, т.е. она симметрична относительно оси Oy, поэтому далее будем исследовать функцию на интервале \((3;+\infty) \), график функции на интервале \((-\infty; -3)\) получим путем симметричного переноса графика, полученного на интервале \((3;+\infty) \) относительно оси Oy.
4. Нули функции (точки пересечения с осью Ox). Интервалы знакопостоянства функции.
точка пересечения с осью Ox: приравняем \(y=0\), получим \(\ln(x^2-9)= 0 => x^2-9=1 => x_1 = \sqrt{10}, x_2 = -\sqrt{10} \) , точки пересечения с осью Ox две, одна из них попадает в рассматриваемый интервал \((3;+\infty) \). Координаты точки пересечения с осью Ox \(( \sqrt{10}; 0)\)
Интервалы знакопостоянства функции. Получили два интервала знакопостоянства на ОДЗ.
интервал \((3; \sqrt{10})\) найдем значение функции в любой точке \( f(3.1) = \ln((3.1)^2-9) < 0 \), на этом интервале функция отрицательная \(f(x) < 0 \), т.е. функция находится ниже оси Ox
интервал \(( \sqrt{10}; + \infty)\) найдем значение функции в любой точке \( f(4) = \ln((4)^2-9) > 0 \), на этом интервале функция положительная \(f(x) > 0 \), т.е. функция находится выше оси Ox
5. Точки пересечения с осью Oy: для этого нужно приравнять \(x=0\), точек пересечения с осью Oy нет, т.к. эта точка не попадает в ОДЗ.
6. Интервалы монотонности. Экстремумы функции.
Найдем критические (стационарные) точки, для этого найдем первую производную и приравняем ее к нулю $$y' = ( \ln(x^2-9))' = \frac{2x}{ x^2-9} $$ приравняем к 0 $$ \frac{2x}{ x^2-9} = 0 => x =0$$ Стационарная точка \( x= 0 \) не попадает в ОДЗ. Функция не имеет критических (стационарных) точек, т.е. нет точек возможного экстремума функции.
Интервалы монотонности.
Функция не имеет критических точек на ОДЗ, поэтому монотонность будем рассматривать на интервалах ОДЗ.
интервал \((3; +\infty)\) найдем значение первой производной в любой точке интервала \(f(4) =\frac{2*4}{ 4^2-9} > 0\), на этом интервале функция возрастает.
Экстремумы функции.
Достаточным условием существования экстремума является изменение знака производной при переходе через критическую точку.
Критических точек нет, значит нет и экстремумов.
7. Интервалы выпуклости и вогнутости. Точки перегиба.
Для нахождения интервалов выпуклости и вогнутости найдем вторую производную функции и приравняем ее к нулю $$y'' = ( \frac{2x}{ x^2-9 })'= \frac{2(x^2-9) - 4x^2}{ (x^2-9 )^2 } = -2\frac{2x^2 + 9}{ (x^2-9 )^2 } $$ При всех значениях \(x\) из ОДЗ вторая производная меньше нуля.
\(f''(x) < 0 \) - функция выпуклая вверх (вогнутая).
Точки перегиба.
Точек перегиба нет, т.к. вторая производная не меняет знак.
8. Асимптоты.
Наклонная асимптота.
Для того, чтобы график функции \(у= \ln(x^2-9) \) при \(x \to \infty\) имел наклонную асимптота \(y = kx+b\), необходимо и достаточно, чтобы существовали два предела $$\lim_{x \to +\infty}=\frac{f(x)}{x} =k $$находим его $$ \lim_{x \to +\infty} \frac{\ln(x^2-9)}{x} = \frac{ \infty}{ \infty} =$$ разрешаем неопределенность по правилу Лопиталя $$ = \lim_{x \to +\infty} \frac{ (\ln(x^2-9))'}{x'} = \lim_{x \to +\infty} \frac{2x}{x^2-9} = 0 => k=0 $$ получили, что график функции наклонной асимптоты не имеет.
Горизонтальная асимптота: для того, чтобы существовала горизонтальная асимптота, необходимо, чтобы существовал предел $$\lim_{x \to +\infty}f(x) = b$$ найдем его $$\lim_{x \to +\infty} ( \ln(x^2-9) ) = \infty$$ горизонтальной асимптоты нет .
Вертикальная асимптота. точек разрыва нет, поэтому нет и вертикальный асимптота.
9. Поведение функции на границах ОДЗ.
Рассмотрим поведение функции на границе ОДЗ \( x = 3\)
$$ \lim_{x \to 3+0} \ln(x^2-9) = -\infty $$ в окрестности правой границы ОДЗ график функции стремится в \( - \infty\)
10. График функции.