1. Уравнения сторон треугольника.
Даны три вершины треугольника, поэтому уравнения сторон будем искать ка уравнение прямой, проходящей через две заданные точки \( \frac{x-x_1}{x_2-x_1} = \frac{y-y_1}{y_2-y_1} \quad (1) \) Подставляем координаты вершин:
уравнение стороны AB, при известных координатах вершины A(-4;1) и B(4;0) $$AB \quad \frac{x+4}{4+4} = \frac{y-1}{0-1} => y = -\frac{1}{8}x + \frac{1}{2}$$
уравнение стороны AC, при известных координатах вершины A(-4;1) и C(5;6) $$AC \quad \frac{x+4}{5+4} = \frac{y-1}{6-1} => y = \frac{5}{9}x + \frac{29}{9}$$
уравнение стороны BC, при известных координатах вершины B(4;0) и C(5;6) $$CB \quad \frac{x-4}{5-4} = \frac{y-0}{6-0} => y = 6x - 24$$
2. Уравнение медианы CK.
Для нахождения уравнения медианы известны координаты одной точки C(5;6), а координаты второй точки K найдем как из свойства медианы - медиана делит отрезок AB на две равные части, т.е. нужно найти середину расстояния между точками A(-4;1) и B(4;0), рассчитаем координаты точки \(K( \frac{x_2+x_1}{2}; \frac{y_2+y_1}{2}) => K( \frac{4-4}{2}; \frac{0+1}{2}) =>\)
координаты точки \(K(0; \frac{1}{2})\)
Подставляем координаты обеих точек в уравнение прямой, проходящей через две заданные точки (1) и получаем $$ \frac{x-5}{0-5} = \frac{y-6}{ \frac{1}{2}-6} => y = \frac{11}{10}x + \frac{1}{2}$$
3. Уравнение прямой \( BM||AC\)
Из условия известно, что прямая BM проходит через точку B(4;0) и имеет такое же направление, что и прямая AC. Две прямые параллельны, если их угловые коэффициенты равны \(k_{MB} = k_{AC} = \frac{5}{9} \quad (2)\). Для нахождения прямой BM воспользуемся уравнением прямой, проходящей через заданную точку в заданном направлении \( y - y_0 = k(x - x_0)\). Подставляем координаты точки и угловой коэффициент $$ y - 0 = \frac{5}{9}(x - 4) => y = \frac{5}{9}x - \frac{20}{9}$$
4. Уравнение высоты AE.
Высота AE опущена из вершины A на сторону BC, т.е. из условия известна одна координата точки A(-4;1) и направление - прямая перпендикулярна прямой BC. Воспользуемся свойством угловых коэффициентов перпендикулярных прямых: \(k_1 = -\frac{1}{k_2}\). Найдем угловой коэффициент \(k_{AE} = -\frac{1}{k_{BC}} = -\frac{1}{6}\). Найдем уравнение прямой AE для этого воспользуемся уравнением прямой проходящей через заданную точку в заданном направлении (2), получим $$ y - 1 = -\frac{1}{6}(x + 4) => y = -\frac{1}{6}x + \frac{1}{3}$$
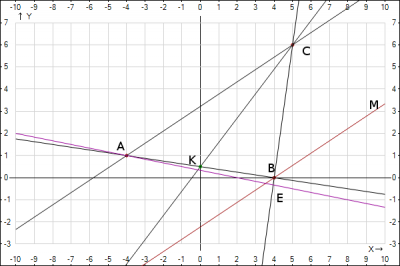
5. Наносим на декартовую систему координат полученные уравнения и координаты точек.