Побудувати криву \( x^2+y^2-8x=0 \).
1. Запишемо рівняння кривої в канонічному вигляді.
В даному рівнянні є тільки члени другого і першого ступеня (немає змішаного твори), тому канонічне рівняння будемо отримувати методом виділення повного квадрата.
$$ x^2+y^2-8x=0 = > $$ доповнюємо члени в дужках до повного квадрата $$ (x^2 -2*4x+16-16)+y^2=0 => (x -4)^2-16+y^2=0 => $$ Отримали рівняння кола. Як відомо канонічне рівняння кола \( (x-a)^2 + (y-b)^2 = R^2 \), з центром в точці \(O(a;b)\) і радіусом \(R\) $$ (x -4)^2 + y^2 = 16 => \quad (1) $$
2. Запишемо координати центру і радіус.
Розглянемо отримане рівняння кола \( (x -4)^2 + y^2 = 4^2 \) з рівняння видно, що координата центру еліпса \(O (4; 0)\) .
Також з рівняння кола визначимо радіус \(R = 4\).
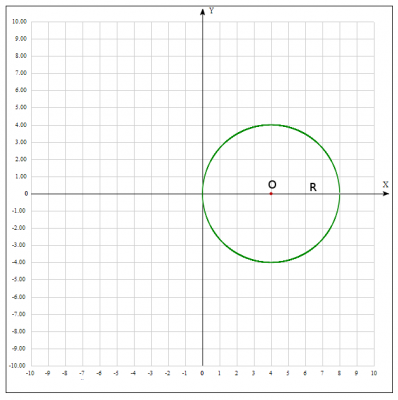
3. Будуємо малюнок: