Исследовать функцию $y = \frac{x}{x^2-4}$ и построить график.

1. Найдем область определения функции. Областью определения будут все значения $x$ , кроме $x^2 = 4 => x = \pm 2$. Т.о. областью определения $D_f = \forall x \in  (-\infty; -2) \cup (-2;2) \cup (2;+\infty))$. Исследуем поведение функции на концах интервалов $$\lim_{x \to -\infty}\frac{x}{x^2-4} = \lim_{x \to -\infty}\frac{\frac{1}{x}}{1-\frac{4}{x^2}} = \frac{0_{-0}}{1-0} = 0_{-0}$$ $$\lim_{x_{-0} \to -2}\frac{x}{x^2-4} = \frac{-2}{4_{+0}-4} = \frac{-2}{0_{+0}} =  -\infty$$ $$\lim_{x_{+0} \to -2}\frac{x}{x^2-4} = \frac{-2}{4_{-0}-4} = \frac{-2}{0_{-0}}= +\infty$$ $$\lim_{x_{-0} \to 2}\frac{x}{x^2-4} = \frac{-2}{4_{-0}-4} = \frac{-2}{0_{-0}}= +\infty$$ $$\lim_{x_{+0} \to 2}\frac{x}{x^2-4} = \frac{-2}{4_{+0}-4} = \frac{-2}{0_{+0}}= -\infty$$ $$\lim_{x \to \infty}\frac{\frac{1}{x}}{1-\frac{4}{x^2}} = \frac{0_{+0}}{1-0} = 0_{+0}$$

2. Найдем точки пересечения с осями координат $Ox$ и $Oy$.
Точка пересечения с осью $Ox$: $y = 0 => \frac{x}{x^2-4} =0 => x=0$, точка пересечения с осью имеет координаты $(0;0)$
Точки пересечения с осью $Oy$: $x = 0 =>y= \frac{x}{x^2-4} => y= \frac{0}{0^2-4} => y=0$, точка пересечения с осью имеет координаты $(0;0)$

3. Исследуем функцию на четность $$f(-x)= \frac{-x}{(-x)^2-4} = - \frac{x}{x^2-4} = -f(x)$$ получили, что функция нечетная, т.е. она симметричная относительно начала координат.

4.Исследуем функцию на экстремумы и монотонность. Необходимым условием существования экстремума является равенство первой производной 0 $f'(a) = 0$. Вычислим первую производную и найдем стационарные точки (точки $a$ в которых $f'(a) =0$ первая производная равно 0, это могут быть кочки экстремумов и точки перегибов) $$y'= (\frac{x}{x^2-4})' = \frac{(x'*(x^2-4) - x*(x^2-4)')}{(x^2-4)^2} = \frac{(x^2-4 - x*2x)}{(x^2-4)^2} = -\frac{(x^2+4)}{(x^2-4)^2}$$ приравняем первую производную к 0 $y' = -\frac{(x^2+4)}{(x^2-4)^2} = 0$ из уравнения видно, что $x^2+4 \ne 0$, т.е. первая производная ни при каких значениях $x$ не будет равна 0, т.е. на интервалах обрасти определения не меняет свою монотонность и у нее нет экстремумов. Анализируя первую производную видно, что числитель и знаменатель на всей области допустимых значений больше 0, а знак "-" указывает, что производная всегда отрицательная. Вывод: функция убывающая на всех участках области определения.

5.Исследуем функцию на выпуклость и наличие точек перегиба. Для этого найдем вторую производную $$(f'(x))' = (-\frac{x^2+4}{(x^2-4)^2})' = -\frac{(x^2+4)'*(x^2-4)^2 - (x^2+4)*((x^2-4)^2)'}{(x^2-4)^4}=$$ $$=-\frac{2x*(x^2-4)^2 - (x^2+4)*2(x^2-4)*2x}{(x^2-4)^4}=-\frac{2x*((x^2-4) - 2*(x^2+4))}{(x^2-4)^3}=$$ $$-\frac{2x*(x^2-4 - 2*x^2-8)}{(x^2-4)^3}=\frac{2x*(x^2+4)}{(x^2-4)^3}$$ Найдем точки перегиба. Необходимым условием существования точки перегиба является равенство второй производной 0 $f''(a) =0$. Приравняем вторую производную к 0 $$\frac{2x*(x^2+4)}{(x^2-4)^3} = 0 => x=0$$ Достаточным условием существования перегиба является изменение знака второй производной при переходе через точку $f''(a)$. Получим знак второй производной в окрестности точки $a = x= 0$, слева от точки $x=0$ $$f''(-1) = \frac{2x*(x^2+4)}{(x^2-4)^3} = \frac{2*(-1)*((-1)^2+4)}{((-1)^2-4)^3} >0$$ функция выпукла вниз, справа от точки $x=0$ $$f''(1) = \frac{2x*(x^2+4)}{(x^2-4)^3} = \frac{2*1*(1^2+4)}{(1^2-4)^3} < 0$$ ,  функция выпукла вверх. Получили, что в точке $(0;0)$ вторая производная меняет знак с "+" на "-", т.е. эта точка является точкой перегиба.

Рассмотрим выпуклость графика функции на оставшихся интервалах
  $(-\infty; -2)$: $f''(-3) = \frac{2x*(x^2+4)}{(x^2-4)^3} = \frac{2(-3)*((-3)^2+4)}{((-3)^2-4)^3} < 0$ - функция выпукла вверх
  $(2; +\infty)$: $f''(3) = \frac{2x*(x^2+4)}{(x^2-4)^3} = \frac{23*(3^2+4)}{(3^2-4)^3} > 0$ - функция выпукла вниз

6. Найдем асимптоты графика функции. При изучении области определения функции и поведения ее на концах интервалов области определения было получено, что $$\lim_{x_{-0} \to -2}\frac{x}{x^2-4} = -\infty$$ $$\lim_{x_{+0} \to -2}\frac{x}{x^2-4} = + \infty$$ $$\lim_{x_{-0} \to 2}\frac{x}{x^2-4} = -\infty$$ По определению вертикальной асимптоты: прямая $x=a$, является вертикальной асимптотой графика функции $y = f(x)$, если хотя бы один из пределов $\lim_{x \to a_{+0}}$ или $\lim_{x \to a_{-0}}$ равен $+\infty$ или $-\infty$. Т.о. прямые $x=-2;x=2$ являются вертикальными асимптотами.

Проверим имеет ли график функции наклонную асимптоту. Найдем предел $$\lim_{x \to +\infty}  \frac{f(x)}{x} = k$$ где $k$ - угловой коэффициент наклонной асимптоты (прямой). $$\lim_{x \to +\infty} \frac{\frac{x}{x^2-4}}{x} = \lim_{x \to +\infty} \frac{1}{x^2-4} = 0 => k = 0$$ наклонной асимптоты график функции не имеет.

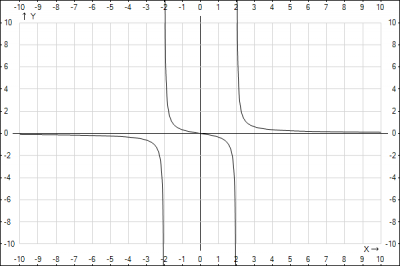
7. Построим график функции.
- наносим вертикальные асимптоты $x=-2; x=2$
- наносим точку пересечения с осями $(0;0)$
- на интервале $(-\infty; -2)$ график асимптотически приближается к оси $Ox$ при $x \to -\infty$ снизу, далее монотонно убывает с выпуклостью вверх и при приближении к вертикальной асимптоты $x = -2$ стремится к $-\infty$
- на интервале $(-2;2)$ от вертикальной асимптоты $x = -2$ график от $+\infty$ монотонно убывает с выпуклостью вниз до точки $(0;0)$, где меняет выпуклость, становится выпуклой вверх, продолжает убывать асимптотически приближаясь $y \to -\infty$ к асимптоте $x=2$
- на интервале  $(2;+\infty)$ от вертикальной асимптоты $x = 2$ график от $+\infty$ монотонно убывает с выпуклостью вниз, асимптотически приближаясь к оси $Ox$ сверху

Строим график функции