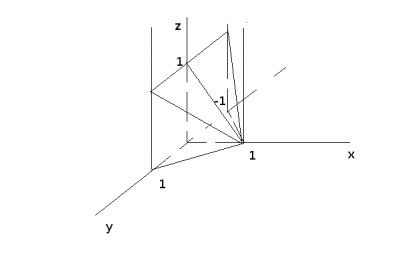
Решение: Вычислим интеграл $$\int\int_V\int(x+z)dxdydz$$ где область интегрирования V - четырехугольная пирамида (см. рис. 1), ограниченная плоскостями $$\begin{cases}x+y = 1\\x-y =1\\x+z =1\\z=0\\x=0\end{cases}$$ Нарисуем эту область
\(x+y = 1\) - плоскость, параллельная оси Oz, пересекается с плоскостью XY по прямой \(x+y = 1\) и пересекает оси \((0;1), (1;0)\)
\(x-y = 1\) - плоскость, параллельная оси Oz, пересекается с плоскостью XY по прямой \(x-y = 1\) и пересекает оси \((0;-1), (1;0)\)
\(x+z = 1\) - плоскость, параллельная оси Oy, пересекается с плоскостью XZ по прямой \(x+z = 1\) и пересекает оси \((0;1), (1;0)\)
\(z = 0\) - плоскость XY
\(x = 0\) - плоскость YZ
Для нахождения тройного интеграла воспользуемся следующей формулой:
Если область интегрирования \(V\) определяется неравенства \(x_1 \leq x \leq x_2\), \(y_1(x) \leq y(x) \leq y_2(x)\), \(z_1(x,y) \leq z \leq z_2(x,y)\), где \(y_1(x), y_2(x), z_1(x,y), z_2(x,y)\) - непрерывные функции своих аргументов, то тройной интеграл вычисляется по формуле $$\int\int_{V}\int f(x,y,z)dxdydz = \int_{x_1}^{x_2}dx\int_{y_1(x)}^{y_2(x)}dy\int_{z_1(x,y)}^{z_2(x,y)}f(x,y,z)dz$$ область \(V\) ограничена сверху плоскостью \(z = z_2(x,y)\), снизу - поверхностью \(z = z_1(x,y)\), а с боков - цилиндрической поверхностью с образующими, параллельными оси Oz, вырезающей на плоскости Oxy \(S_{xy}\), определенную неравенствами \(x_1 \leq x \leq x_2\), \(y_1(x) \leq y \leq y_2(x)\). Обращаю внимание, что порядок интегрирования может быть любым.
Алгоритм вычисления тройного интеграла:
1. Расставим пределы интегрирования.
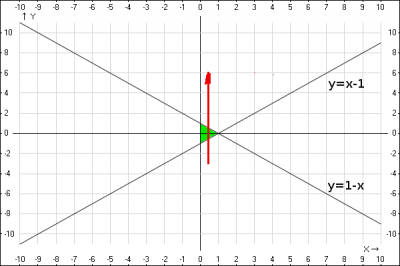
Рассмотрим плоскость XY (см. рис. 2). На этой плоскости вырезается фигура (зеленый треугольник), определяемая неравенствами:
по переменной \(x\) \(0 \leq x \leq 1 \),
по переменной \(y\) определяем по стрелке на рисунке, получаем \( x-1 \leq y \leq 1 - x \).
Рассмотрим переменную \(z\). Область снизу ограничена плоскостью \(z=0\), а сверху плоскостью \(x+z=1 => z = 1-x\), получаем \(0 \leq z \leq 1-x\).
2. Вычисляем тройной интеграл при известных границах $$\int\int_V\int(x+z)dxdydz = \int_0^1dx\int_{x-1}^{1-x}dy\int_0^{1-x}(x+z)dz = \quad (2)$$
вычисляем интеграл \( \int_0^{1-x}(x+z)dz = \) где \(z\) - переменная интегрирования, а \(x\) - постоянная, получаем \( \int_0^{1-x}(x+z)dz = xz + \frac{1}{2}z^2 |_0^{1-x} = \) \(= x(1-x)+\frac{1}{2}(1-x)^2 = \frac{1}{2}(1-x)(1+x) = \frac{1}{2}(1-x^2) \) подставляем в (2) $$ = \int_0^1dx\int_{x-1}^{1-x}\frac{1}{2}(1-x^2)dy = \frac{1}{2} \int_0^1dx\int_{x-1}^{1-x}(1-x^2)dy = \quad (3)$$
вычисляем интеграл \( \int_{x-1}^{1-x}(1-x^2)dy = \) где \(y\) - переменная интегрирования, а \(x\) - постоянная, получаем \( = (1-x^2) \int_{x-1}^{1-x}dy = (1-x^2)y|_{x-1}^{1-x} = \) \((1-x^2)(1-x -x+1) = 2(1-x^2)(1-x) \) подставляем в (3) $$ =\frac{1}{2} \int_0^122(1-x^2)(1-x) dx = \int_0^1(1-x^2-x+x^3)dx = $$$$ = x- \frac{1}{3}x^2 - \frac{1}{2}x^2+\frac{1}{4}x^4|_0^1 = 1- \frac{1}{3} - \frac{1}{2}+\frac{1}{4} = \frac{5}{12}$$
Ответ: тройной интеграл равен \(V = \frac{5}{12} \)



