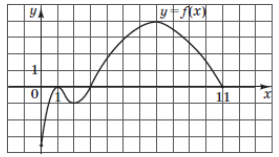
–Ч–∞–≤–і–∞–љ–љ—П: –Э–∞ —А–Є—Б—Г–љ–Ї—Г –Ј–Њ–±—А–∞–ґ–µ–љ–Њ –≥—А–∞—Д—Ц–Ї —Д—Г–љ–Ї—Ж—Ц—Ч \(y = f(x)\), –≤–Є–Ј–љ–∞—З–µ–љ–Њ—Ч –љ–∞ –њ—А–Њ–Љ—Ц–ґ–Ї—Г [0;11] —В–∞ –і–Є—Д–µ—А–µ–љ—Ж—Ц–є–Њ–≤–∞–љ–Њ—Ч –љ–∞ –њ—А–Њ–Љ—Ц–ґ–Ї—Г (0;11). –£—Б—В–∞–љ–Њ–≤—Ц—В—М –≤—Ц–і–њ–Њ–≤—Ц–і–љ—Ц—Б—В—М –Љ—Ц–ґ —З–Є—Б–ї–Њ–Љ (1-4) —В–∞ –њ—А–Њ–Љ—Ц–ґ–Ї–Њ–Љ (–Р-–Ф), —П–Ї–Њ–Љ—Г –љ–∞–ї–µ–ґ–Є—В—М —Ж–µ —З–Є—Б–ї–Њ.
¬†$$\begin{array}{|l|c|} \hline \\ –І–Є—Б–ї–Њ & –Я—А–Њ–Љ—Ц–ґ–Њ–Ї¬† \\
\hline¬† \\ 1. f(8) &¬† –Р \quad (-\infty; -2]¬†¬† \\
\hline \\ 2.¬† f'(7)¬† & –С \quad¬† ( -2; -0,5]¬†¬† \\
\hline \\ 3. –љ–∞–є–Љ–µ–љ—И–µ¬†\quad –Ј–љ–∞—З–µ–љ–љ—П¬†\quad —Д—Г–љ–Ї—Ж—Ц—Ч¬†\quad y = f(x) \\ –љ–∞\quad —Ч—Ч\quad –Њ–±–ї–∞—Б—В—Ц\quad –≤–Є–Ј–љ–∞—З–µ–љ–љ—П & –Т \quad¬† ( -0,5; 2]¬†¬† \\
\hline \\ 4.¬† \int_1^3 f(x) dx¬† & –У \quad (2; 4]¬†¬† \\
\hline \\ & –Ф \quad (4; +\infty)¬† \\
\hline \end{array}$$
–†—Ц—И–µ–љ–љ—П: –љ–∞–љ–µ—Б–µ–Љ –≤—Б–µ –≤–Њ–њ—А–Њ—Б—Л –Ј–∞–і–∞–љ–Є—П –љ–∞ —А–Є—Б. –і–ї—П —Г–њ—А–Њ—Й–µ–љ–Є—П –∞–љ–∞–ї–Є–Ј–∞
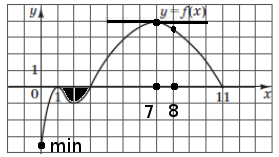
1. \(f(8)\) - –љ–∞–є—В–Є –Ј–љ–∞—З–µ–љ–Є–µ —Д—Г–љ–Ї—Ж–Є–Є –≤ —В–Њ—З–Ї–µ \(x = 8\). –Э–∞ –≥—А–∞—Д–Є–Ї–µ –љ–∞—Е–Њ–і–Є–Љ –Ј–љ–∞—З–µ–љ–Є–µ —Д—Г–љ–Ї—Ж–Є–Є –њ—А–Є \(x = 8 => y = 3,5\)
–Т—Ц–і–њ–Њ–≤—Ц–і—М: \(f(8) -> [2;4)\)
2. \(f'(7)\) - –љ–∞–є—В–Є –Ј–љ–∞—З–µ–љ–Є–µ –њ—А–Њ–Є–Ј–≤–Њ–і–љ–Њ–є —Д—Г–љ–Ї—Ж–Є–Є –≤ —В–Њ—З–Ї–µ \(x = 7\). –У–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є–є —Б–Љ—Л—Б–ї –њ—А–Њ–Є–Ј–≤–Њ–і–љ–Њ–є –≤ —В–Њ—З–Ї–µ - —В–∞–љ–≥–µ–љ—Б —Г–≥–ї–∞ –љ–∞–Ї–ї–Њ–љ–∞ –Ї–∞—Б–∞—В–µ–ї—М–љ–Њ–є –≤ —Н—В–Њ–є —В–Њ—З–Ї–µ. –Ш–Ј —А–Є—Б—Г–љ–Ї–∞ –≤–Є–і–љ–Њ, —З—В–Њ –≤ —Н—В–Њ–є —В–Њ—З–Ї–µ —Г–≥–Њ–ї —А–∞–≤–µ–љ \(0^0\), –∞ \(\mbox{tg0}^0 = 0\)
–Т—Ц–і–њ–Њ–≤—Ц–і—М: \(f'(7) -> (-0,5;2]\)
3. –Э–∞–є–Љ–µ–љ—И–µ –Ј–љ–∞—З–µ–љ–љ—П —Д—Г–љ–Ї—Ж—Ц—Ч \(y = f(x)\) –љ–∞ —Ч—Ч –Њ–±–ї–∞—Б—В—Ц –≤–Є–Ј–љ–∞—З–µ–љ–љ—П. –Э–∞–Є–Љ–µ–љ—М—И–µ–µ –Ј–љ–∞—З–µ–љ–Є–µ —Д—Г–љ–Ї—Ж–Є–Є –љ–∞ –Њ–±–ї–∞—Б—В–Є –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П - —В–Њ—З–Ї–∞ —Б —Б–∞–Љ—Л–Љ –Љ–∞–ї–µ–љ—М–Ї–Є–Љ –Ј–љ–∞—З–µ–љ–Є–µ–Љ y. –Э–∞ –≥—А–∞—Д–Є–Ї–µ —Н—В–Њ —В–Њ—З–Ї–∞ \((0;-3,5)\)
–Т—Ц–і–њ–Њ–≤—Ц–і—М: \( (-\infty; -2]\)
4. \(\int_1^3 f(x) dx\) - —Н—В–Њ –њ–ї–Њ—Й–∞–і—М –Ј–∞—И—В—А–Є—Е–Њ–≤–∞–љ–љ–Њ–є —Д–Є–≥—Г—А—Л \(x \in [1;3]\). –Э–∞ –≥—А–∞—Д–Є–Ї–µ –≤–Є–і–љ–Њ, —З—В–Њ –Ј–∞—И—В—А–Є—Е–Њ–≤–∞–љ–љ–∞—П –њ–ї–Њ—Й–∞–і—М —А–∞–≤–љ–∞ –Њ–Ї–Њ–ї–Њ 1, –љ–Њ, —В.–Ї. –≥—А–∞—Д–Є–Ї –љ–∞—Е–Њ–і–Є—В—Б—П –љ–Є–ґ–µ –Њ—Б–Є \(x\), —В–Њ –Є–љ—В–µ–≥—А–∞–ї –њ—А–Є–Љ–µ—В –Њ—В—А–Є—Ж–∞—В–µ–ї—М–љ–Њ–µ –Ј–љ–∞—З–µ–љ–Є–µ, —В.–µ. \(\int_1^3 f(x) dx \approx -1\)
–Т—Ц–і–њ–Њ–≤—Ц–і—М: \( (-2; -0,5]\)
¬†–њ–Њ–њ–µ—А–µ–і–љ—Ф –Ј–∞–≤–і–∞–љ–љ—П вДЦ 23 ¬†¬†¬† –љ–∞—Б—В—Г–њ–љ–µ –Ј–∞–≤–і–∞–љ–љ—П вДЦ 25
