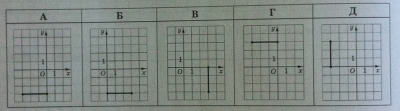
Завдання: На рисунку зображено відрізок \(d\) на координатній площині \(xy\). Установіть відповідність між відрізком \((1-4)\) на рисунком \((А-Д)\), на якому він зображений.
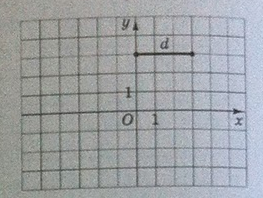
Варіант відповіді:
1. відрізок, симетричний відрізку \(d\) відносно осі \(x\)
2. відрізок, симетричний відрізку \(d\) відносно осі \(y\)
3. відрізок, симетричний відрізку \(d\) відносно точки \(O\)
4. відрізок, який переходить відрізок \(d\) внаслідок повороту навколо точки \(O\) на кут \(90^0\) проти руху годинникової стрілки
Рішення:
Симметрия относительно прямой. Точки \(А\) и \(А_1\) называются симметричными относительно прямой \(a\) (ось симметрии), если прямая a проходит через середину отрезка \(АА_1\) и перпендикулярна к этому отрезку.
В задании рассматривается симметрия относительно осей координат. Рассмотрим признаки симметрии относительно осей.
a) Координаты точек симметричных относительно оси \(Ox\) \(A(x;y)\) \(A_1(x;-y)\)
b) Координаты точек симметричных относительно оси \(Oy\) \(A(x;y)\) \(A_1(-x;y)\)
c) Координаты точек симметричных начала координат \(Ox\) \(A(x;y)\) \(A_1(-x;-y)\)
Для анализа симметрии возьмем координаты концов отрезка \(d\), получим \(A(0;3); \quad B(3;3)\)
1. відрізок, симетричний відрізку \(d\) відносно осі \(x\)
Согласно п. a) получим координаты точек симметричных относительно оси \(Ox\): \(A_1(0;-3); \quad B_1(3;-3)\) - вариант ответа \(Б\)
2. відрізок, симетричний відрізку \(d\) відносно осі \(y\)
Согласно п. b) получим координаты точек симметричных относительно оси \(Oy\): \(A_1(0;3); \quad B_1(-3;3)\) - вариант ответа \(Г\)
3. відрізок, симетричний відрізку \(d\) відносно точки \(O\)
Согласно п. c) получим координаты точек симметричных относительно точки \(O\): \(A_1(0;-3); \quad B_1(-3;-3)\) - вариант ответа \(А\)
4. відрізок, який переходить відрізок \(d\) внаслідок повороту навколо точки \(O\) на кут \(90^0\) проти руху годинникової стрілки
При повороте отрезка на \(90^0\) вокруг точки \(O\) против часовой стрелки получим координаты \(A_1(-3;0); \quad B_1(-3;3)\) - вариант ответа \(Д\)
Відповідь: $$\begin{array}{|c|c|c|}\hline & А & Б & В & Г & Д\\ \hline 1& & X & & \\ \hline 2& & & X & \\ \hline 3& X & & & \\ \hline 4& & & & & X \\ \hline \end{array}$$

