–Ч–Љ—Ц—Б—В –Ј–∞–≤–і–∞–љ–љ—П : –Ь–∞–ї–µ–љ—М–Ї–Є–є –Ї–∞–Љ—Ц–љ–µ—Ж—М, —П–Ї–Є–є –Ї–Є–љ—Г–ї–Є –Ј—Ц —И–≤–Є–і–Ї—Ц—Б—В—О \(v_{0}\) –њ—Ц–і –Ї—Г—В–Њ–Љ \(\alpha\) –і–Њ –≥–Њ—А–Є–Ј–Њ–љ—В—Г, –ї–µ—В–Є—В—М –љ–∞–і –і–Ј–µ—А–Ї–∞–ї—М–љ–Њ—О –њ–Њ–≤–µ—А—Е–љ–µ—О –Њ–Ј–µ—А–∞. –Т–Є–Ј–љ–∞—З—В–µ —И–≤–Є–і–Ї—Ц—Б—В—М —А—Г—Е—Г –Ї–∞–Љ—Ц–љ—Ж—П –≤—Ц–і–љ–Њ—Б–љ–Њ –є–Њ–≥–Њ –Ј–Њ–±—А–∞–ґ–µ–љ–љ—П —Г –≤–Њ–і–љ–Њ–Љ—Г –і–Ј–µ—А–Ї–∞–ї—Ц, –Ї–Њ–ї–Є –Ї–∞–Љ—Ц–љ–µ—Ж—М –њ–µ—А–µ–±—Г–≤–∞—Ф –≤ –љ–∞–є–≤–Є—Й—Ц–є —В–Њ—З—Ж—Ц —Б–≤–Њ—Ф—Ч —В—А–∞—Ф–Ї—В–Њ—А—Ц—Ч.
–Т—Ц–і–њ–Њ–≤—Ц–і—Ц –і–Њ –Ј–∞–≤–і–∞–љ–љ—П:
–Р |
–С |
–Т |
–У |
|
|
\(v_{0}\sin \alpha\) |
\(v_{0}\cos \alpha\) |
\(v_{0}\) |
–Ґ–µ–Њ—А—Ц—П –і–Њ –Ј–∞–≤–і–∞–љ–љ—П: –Ь–∞–ї–µ–љ—М–Ї–Є–є –Ї–∞–Љ—Ц–љ–µ—Ж—М –Ї–Є–љ—Г—В–Њ –њ—Ц–і –Ї—Г—В–Њ–Љ ќ± –і–Њ –≥–Њ—А–Є–Ј–Њ–љ—В—Г –Ј—Ц —И–≤–Є–і–Ї—Ц—Б—В—О ѕЕќњ. –£ –≤—Б—Ц—Е –Ј–∞–≤–і–∞–љ–љ—П—Е –љ–∞ –Ї—Ц–љ–µ–Љ–∞—В–Є–Ї—Г –Њ–њ–Њ—А–Њ–Љ –њ–Њ–≤—Ц—В—А—П –љ–µ—Е—В—Г—О—В—М. –Ф–ї—П –Њ–њ–Є—Б—Г —А—Г—Е—Г –љ–µ–Њ–±—Е—Ц–і–љ–Њ –≤–Є–±—А–∞—В–Є –і–≤—Ц –Њ—Б—Ц –Ї–Њ–Њ—А–і–Є–љ–∞—В - \(Ox\) —Ц \(Oy\) (—А–Є—Б. 1). –Я–Њ—З–∞—В–Њ–Ї –≤—Ц–і–ї—Ц–Ї—Г —Б—Г–Љ—Ц—Б–љ–Є–є –Ј –њ–Њ—З–∞—В–Ї–Њ–≤–Є–Љ –њ–Њ–ї–Њ–ґ–µ–љ–љ—П–Љ —В—Ц–ї–∞. –Я—А–Њ–µ–Ї—Ж—Ц—Ч –њ–Њ—З–∞—В–Ї–Њ–≤–Њ—Ч —И–≤–Є–і–Ї–Њ—Б—В—Ц –љ–∞ –Њ—Б—Ц \(Oy\) —Ц \(Ox\):
$$ v_{y} =v_{o}\sin{\alpha} $$$$ v_{x} = v_{o}\cos{\alpha} $$
–Я—А–Њ–µ–Ї—Ж—Ц—Ч –њ—А–Є—Б–Ї–Њ—А–µ–љ–љ—П:\( g_{ox} = 0;¬† g_{oy} = -g¬† \) .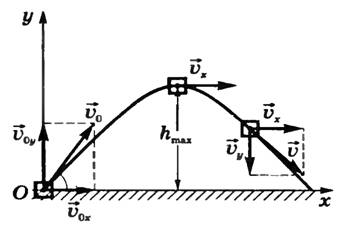 ¬†¬†
  
—А–Є—Б. 1
–Ґ–Њ–і—Ц —А—Г—Е –Ї–∞–Љ—Ц–љ–µ—Ж—П –±—Г–і–µ –Њ–њ–Є—Б—Г–≤–∞—В–Є—Б—П —А—Ц–≤–љ—П–љ–љ—П–Љ–Є:
$$ x = v_{o}\cos{\alpha}*t $$$$ v_{x} = v_{o}\cos{\alpha}$$$$ y = v_{o}\sin{\alpha}*t   -\frac{gt^2}{2}$$$$ v_{y} = v_{o}\sin{\alpha}*t - gt $$
–Ч —Ж–Є—Е —Д–Њ—А–Љ—Г–ї –≤–Є–њ–ї–Є–≤–∞—Ф, —Й–Њ –≤ –≥–Њ—А–Є–Ј–Њ–љ—В–∞–ї—М–љ–Њ–Љ—Г –љ–∞–њ—А—П–Љ–Ї—Г –Ї–∞–Љ—Ц–љ–µ—Ж—М —А—Г—Е–∞—Ф—В—М—Б—П —А—Ц–≤–љ–Њ–Љ—Ц—А–љ–Њ –Ј—Ц —И–≤–Є–і–Ї—Ц—Б—В—О \( v_{ox} = v_{o}\cos{\alpha} \), –∞ —Г –≤–µ—А—В–Є–Ї–∞–ї—М–љ–Њ–Љ—Г - —А—Ц–≤–љ–Њ–њ—А–Є—Б–Ї–Њ—А–µ–љ–µ (–і–Њ –≤–Є—Б–Њ—В–Є \( h_{max}¬† \) - —Г–њ–Њ–≤—Ц–ї—М–љ—О—Ф—В—М—Б—П, –і–∞–ї—Ц –њ–∞–і–∞—Ф –љ–∞ –Ј–µ–Љ–ї—О - –њ—А–Є—Б–Ї–Њ—А—О—Ф—В—М—Б—П).
–Ґ—А–∞—Ф–Ї—В–Њ—А—Ц—Ф—О —А—Г—Е—Г –Ї–∞–Љ—Ц–љ–µ—Ж—П –±—Г–і–µ –њ–∞—А–∞–±–Њ–ї–∞.
–†—Ц—И–µ–љ–љ—П: —И–≤–Є–і–Ї—Ц—Б—В—М —А—Г—Е—Г –Ї–∞–Љ—Ц–љ—Ж—П –≤—Ц–і–љ–Њ—Б–љ–Њ –є–Њ–≥–Њ –Ј–Њ–±—А–∞–ґ–µ–љ–љ—П —Г –≤–Њ–і–љ–Њ–Љ—Г –і–Ј–µ—А–Ї–∞–ї—Ц, –Ї–Њ–ї–Є –Ї–∞–Љ—Ц–љ–µ—Ж—М –њ–µ—А–µ–±—Г–≤–∞—Ф –≤ –љ–∞–є–≤–Є—Й—Ц–є —В–Њ—З—Ж—Ц —Б–≤–Њ—Ф—Ч —В—А–∞—Ф–Ї—В–Њ—А—Ц—Ч
$$ h_{max}   ;  v_{y} = 0 $$.
–Т—Ц–і–њ–Њ–≤—Ц–і—М: –Р: 0.

