–Ч–∞–≤–і–∞–љ–љ—П: –Ю—Б–љ–Њ–≤–Њ—О –њ—Ц—А–∞–Љ—Ц–і–Є —Ф —А–Њ–Љ–±, —В—Г–њ–Є–є –Ї—Г—В —П –Ї–Њ–≥–Њ –і–Њ—А—Ц–≤–љ—О—Ф 120¬∞. –Ф–≤—Ц –±—Ц—З–љ—Ц –≥—А–∞–љ—Ц –њ—Ц—А–∞–Љ—Ц–і–Є, —Й–Њ –Љ—Ц—Б—В—П—В—М —Б—В–Њ—А–Њ–љ–Є —Ж—М–Њ–≥–Њ –Ї—Г—В–∞, –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ—Ц –і–Њ –њ–ї–Њ—Й–Є–љ–Є –Њ—Б–љ–Њ–≤–Є, –∞ –і–≤—Ц —Ц–љ—И—Ц –±—Ц—З–љ—Ц –≥—А–∞–љ—Ц –љ–∞—Е–Є–ї–µ–љ—Ц –і–Њ –њ–ї–Њ—Й–Є–љ–Є –Њ—Б–љ–Њ–≤–Є –њ—Ц–і –Ї—Г—В–Њ–Љ 30¬∞. –Ч–љ–∞–є–і—Ц—В—М –њ–ї–Њ—Й—Г –±—Ц—З–љ–Њ—Ч –њ–Њ–≤–µ—А—Е–љ—Ц –њ—Ц—А–∞–Љ—Ц–і–Є (—Г —Б–Љ2), —П–Ї—Й–Њ —Ч—Ч –≤–Є—Б–Њ—В–∞ –і–Њ—А—Ц–≤–љ—О—Ф 4 —Б–Љ.
–†—Ц—И–µ–љ–љ—П:¬† –і–ї—П —А–µ—И–µ–љ–Є—П –Ј–∞–і–∞—З–Є –љ–∞–Љ –њ–Њ–љ–∞–і–Њ–±–Є—В—Б—П —А–Є—Б—Г–љ–Њ–Ї, –љ–∞—А–Є—Б—Г–µ–Љ –µ–≥–Њ
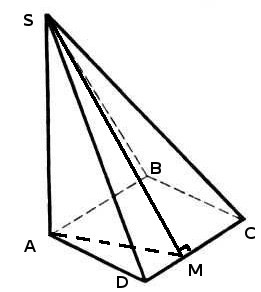
¬†–°–Њ–≥–ї–∞—Б–љ–Њ –Ј–∞–і–∞–љ–Є—П –љ–∞–Љ –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –љ–∞–є—В–Є –њ–ї–Њ—Й–∞–і—М –±–Њ–Ї–Њ–≤–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є. –Я–ї–Њ—Й–∞–і—М –±–Њ–Ї–Њ–≤–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —А–∞–≤–љ–∞ —Б—Г–Љ–Љ–µ –њ–ї–Њ—Й–∞–і–µ–є –≤—Б–µ—Е –±–Њ–Ї–Њ–≤—Л—Е –≥—А–∞–љ–µ–є. –Ч–∞–њ–Є—И–µ–Љ —Н—В–Њ —Г—В–≤–µ—А–ґ–і–µ–љ–Є–µ –≤ –≤–Є–і–µ —Д–Њ—А–Љ—Г–ї—Л $$S_{–±–Њ–Ї} = S_{ASD}+S_{ASB}+S_{BSC}+S_{DSC}$$—А–∞—Б—Б–Љ–Њ—В—А–Є–Љ –±–Њ–ї–µ–µ –і–µ—В–∞–ї—М–љ–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є:
- \(ќФASD\) = \(ќФASB\) - —Н—В–Њ —А–∞–≤–љ—Л–µ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є, —В.–Ї. —Н—В–Њ –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Л–µ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є —Б —А–∞–≤–љ—Л–Љ–Є –Ї–∞—В–µ—В–∞–Љ–Є: \(AS\) - –Њ–±—Й–Є–є –Ї–∞—В–µ—В, –∞ \(AD=AB\) - –Ї–∞–Ї —Б—В–Њ—А–Њ–љ—Л —А–Њ–Љ–±—Л. –Ш–Ј —А–∞–≤–µ–љ—Б—В–≤–∞ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤ —Б–ї–µ–і—Г–µ—В –≤–∞–ґ–љ—Л–є –≤—Л–≤–Њ–і - —А–∞–≤–µ–љ—Б—В–≤–Њ –≥–Є–њ–Њ—В–µ–љ—Г–Ј \(SD=SB\)
- \(ќФBSC\) = \(ќФDSC\) - —Н—В–Њ —А–∞–≤–љ—Л–µ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є –њ–Њ —В—А–µ–Љ —Б—В–Њ—А–Њ–љ–∞–Љ: \(BC=DC\) - –Ї–∞–Ї —Б—В–Њ—А–Њ–љ—Л —А–Њ–Љ–±–∞, \(SD=SB\) - –Ї–∞–Ї —А–∞–≤–љ—Л–µ –≥–Є–њ–Њ—В–µ–љ—Г–Ј—Л —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤ \(ќФASD\) –Є \(ќФASB\), \(SC\) -¬† –Њ–±—Й–∞—П —Б—В–Њ—А–Њ–љ–∞ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤.
–Я—А–Њ–≤–µ–і–µ–Љ —Б–µ–Ї—Г—Й—Г—О —З–µ—А–µ–Ј –Њ—В—А–µ–Ј–Њ–Ї \(SA\) –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ–Њ –Њ—В—А–µ–Ј–Ї—Г \(–Т–°\). –≠—В–Њ –Љ—Л —Б–і–µ–ї–∞–ї–Є, —З—В–Њ–±—Л –њ–Њ–ї—Г—З–Є—В—М –≤—Л—Б–Њ—В—Г¬† \(SM\) —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ \(ќФDSC\) –Є –≤—Л—Б–Њ—В—Г¬† \(AM\) —А–Њ–Љ–±–∞ \(ABCD\). –Ч–∞–њ–Є—И–µ–Љ –њ–ї–Њ—Й–∞–і—М –±–Њ–Ї–Њ–≤–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —Б —Г—З–µ—В–Њ–Љ –≤–≤–µ–і–µ–љ–љ—Л—Е –Њ–±–Њ–Ј–љ–∞—З–µ–љ–Є–є.
–Ъ–∞–Ї –Є–Ј–≤–µ—Б—В–љ–Њ, –њ–ї–Њ—Й–∞–і–Є —А–∞–≤–љ—Л—Е —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤ —А–∞–≤–љ—Л, –њ–Њ—Н—В–Њ–Љ—Г –њ–ї–Њ—Й–∞–і—М –±–Њ–Ї–Њ–≤–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –Љ–Њ–ґ–љ–Њ –њ—А–µ–і—Б—В–∞–≤–Є—В—М –Ї–∞–Ї: $$S_{–±–Њ–Ї} = 2*S_{ќФASD}+2*S_{ќФDSC}$$–≥–і–µ
$$2*S_{ќФASD} = 2*\frac{1}{2}SA*AD = 4*AD$$ \(SA = 4\)
$$2*S_{ќФDSC} = 2*\frac{1}{2}SM*DC = SM*DC$$–≥–і–µ \(AD=DC=a\) - —Б—В–Њ—А–Њ–љ—Л —А–Њ–Љ–±–∞
–Я–Њ–і—Б—В–∞–≤–ї—П–µ–Љ –≤ —Д–Њ—А–Љ—Г–ї—Г –Є –њ–Њ–ї—Г—З–∞–µ–Љ $$S_{–±–Њ–Ї} = 4*a+a*SM$$—В–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –љ–∞–є—В–Є —Б—В–Њ—А–Њ–љ—Г —А–Њ–Љ–±–∞ \(a\) –Є –≤—Л—Б–Њ—В—Г —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ \(ќФDSC\)¬† - \(SM\). –Э–∞–є–і–µ–Љ –≤—Л—Б–Њ—В—Г \(SM\) –Є–Ј —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ \(ќФSAM\). –Ш–Ј —Г—Б–ї–Њ–≤–Є—П –Є–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ —Г–≥–Њ–ї –љ–∞–Ї–ї–Њ–љ–∞ –±–Њ–≥–Њ–≤–Њ–є –≥—А–∞–љ–Є –Ї –Њ—Б–љ–Њ–≤–∞–љ–Є—О —А–∞–≤–µ–љ \(30^0\), —В.–µ. —Г–≥–Њ–ї \(\angle SMA = 30^0\), —В–Њ–≥–і–∞ –Ї–∞—В–µ—В, –ї–µ–ґ–∞—Й–Є–є –њ—А–Њ—В–Є–≤ —Г–≥–ї–∞ \(30^0\) –≤ –і–≤–∞ —А–∞–Ј–∞ –Љ–µ–љ—М—И–µ –≥–Є–њ–Њ—В–µ–љ—Г–Ј—Л, —В.–µ. \(SM = 2 SA = 2*4 = 8\) –Є–ї–Є –њ–Њ –і—А—Г–≥–Њ–Љ—Г \(SA = \sin 30^0*SM = \frac{1}{2}SM => SM = 2*SA = 8\).–Ф–ї—П –љ–∞—Е–Њ–ґ–і–µ–љ–Є—П —Б—В–Њ—А–Њ–љ—Л —А–Њ–Љ–±–∞ –љ–∞–Љ –њ–Њ–љ–∞–і–Њ–±–Є—В—Б—П –Ї–∞—В–µ—В \(AM = \cos 30^0*SM = \frac{\sqrt 3}{2}*8 =4\sqrt 3\)
–Ш—Й–µ–Љ —Б—В–Њ—А–Њ–љ—Г —А–Њ–Љ–±–∞ \(a\). –Т–Њ–Ј–≤—А–∞—Й–∞–µ–Љ—Б—П –Ї —А–Њ–Љ–±—Г. –°–Њ–≥–ї–∞—Б–љ–Њ —Г—Б–ї–Њ–≤–Є—П \(\angle A = 120^0\), —В–Њ–≥–і–∞ —Г–≥–Њ–ї \(\angle D = 180^0 - 120^0 = 60^0\).
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ \(ќФDAM\) —Н—В–Њ –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Л–є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї \(a = AD = \frac{AM}{\sin 60^0} = \frac{4\sqrt 3}{\frac{\sqrt 3}{2}} = 8\)
–Я–Њ–і—Б—В–∞–≤–ї—П–µ–Љ –њ–Њ–ї—Г—З–µ–љ–љ—Л–µ —А–µ–Ј—Г–ї—М—В–∞—В—Л –≤ —Д–Њ—А–Љ—Г–ї—Г –њ–ї–Њ—Й–∞–і–Є –±–Њ–Ї–Њ–≤–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є: $$S_{–±–Њ–Ї} = 4*a+a*SM =¬† 4*8 + 8*8 = 32 + 64 = 96 —Б–Љ^2$$
–Т—Ц–і–њ–Њ–≤—Ц–і—М: 96
¬† –њ–Њ–њ–µ—А–µ–і–љ—Ф –Ј–∞–≤–і–∞–љ–љ—П вДЦ 31 ¬†¬†¬† –љ–∞—Б—В—Г–њ–љ–µ –Ј–∞–≤–і–∞–љ–љ—П вДЦ 33

