Решение:
По данным этой таблицы найдем накопленные частоты, т. е. число значений, которые попали в этот интервал и все предшествующие и накопленные относительные частоты, отношение накопленной частоты \(m_{x_i}\) к объему выборки \(n\) называется накопленные относительные частоты: \(w_i = \frac{m_i}{n}\)
Вычислим объем выборки: \(n=8+5+8+9+12=42\)
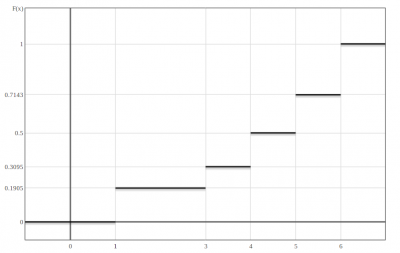
Наименьшая варианта равна: \(x_1=1\), поэтому \(F_n(x)=0\) при \(x ≤ 1\)
Значения \(X < 3\), а именно: \(x_1=1\), наблюдались 8 раз, следовательно, \(F_n(x)=\frac{8}{42}=0.1905\) при \(1 < x ≤ 3\)
Значения \(X < 4\), а именно: \(x_1=1, x_2=3\), наблюдались 13 раз, следовательно, \(F_n(x)=\frac{13}{42}=0.3095\) при \(3 < x ≤ 4\)
Значения \(X < 5\), а именно: \(x_1=1, x_2=3, x_3=4\), наблюдались 21 раз, следовательно, \(F_n(x)=\frac{21}{42}=0.5\) при \(4 < x ≤ 5\)
Значения \(X < 6\), а именно: \(x_1=1, x_2=3, x_3=4, x_4=5\), наблюдались 30 раз, следовательно, \(F_n(x)=\frac{30}{42}=0.7143\) при \(5 < x ≤ 6\)
Т.к. \(X = 6\) - наибольшая варианта, то \(F_n(x)=1\) при \(x > 6\)
$$\begin{array}{|c|c|}\hline x_i& 1& 3 & 4& 5&6&42 \\ \hline m_i& 8& 5 & 8& 9&12&42 \\ \hline \\ m_{x_i}& 0& 0+8=8 & 8+5=13& 13+8=21& 21+9=30&30+12 =42 \\ w_{x_i}& 0& \frac{8}{42}=0.1905 & \frac{13}{42}=0.3095 & \frac{21}{42}=0.5 & \frac{30}{42}=0.7143 &\frac{42}{42}=1 \\ \hline \hline \end{array}$$
Определим эмпирическую функцию \(F_n(x )\) и построим ее график
Эмпирическая функция $$F_n(x)\left[\begin{array}{c} 0 & если & x \leq 1\\ 0.1905 & если & 1 < x \leq 3\\ 0.3095 & если & 3 < x \leq 4\\ 0.5 & если & 4 < x \leq 5\\ 0.7143 & если & 5 < x \leq 6\\ 1 & если & x > 6\\ \end{array}\right.$$
График эмпирической функции