Решение: найдем площадь фигуры, ограниченной параболой \( y=x^2 \) и прямой \(y=\sqrt{x}\) (смотрим рисунок).
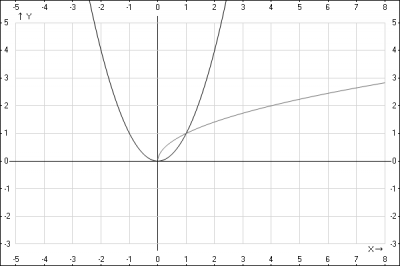
Схема нахождения площади фигуры, ограниченная кривыми.
1. Находим точки пересечения.
Для нахождения точек пересечения составим систему уравнений с учетом ОДЗ корня \(x \geq 0 \) $$ \begin{cases} y=x^2 \\y=\sqrt{x} \\ x \geq 0 \end{cases} => \begin{cases} x^2 - \sqrt{x} = 0 \\y=\sqrt{x} \\ x \geq 0 \end{cases} =>$$$$ \begin{cases} \sqrt{x}(x^{\frac{3}{2}} - 1) = 0 \\y=\sqrt{x} \\ x \geq 0 \end{cases} => \begin{cases} x_1 = 0; x_2=1 \\ y_1=0; y_2 =1 \\ x \geq 0 \end{cases} $$ границы интегрирования по переменной \(x\) равны \([0;1]\)
2. Находим площадь фигуры.
Площадь находится по формуле \(S = \int_a^b[f(x) - g(x)]dx = \int_a^b[y_2 - y_1]dx\)
\(y_2\) - функция выше функции \(y_1\), согласно рисунка \(y_2= \sqrt{x}\), а \(y_1= x^2\). Подставляем в формулу площади $$S = \int_{0}^1[ \sqrt{x} - x^2]dx = $$применим формулу Ньютона-Лейбница \( \int_a^bf(x)dx = F(x)|_a^b = F(b) - F(a)\) , получим $$ = \frac{1}{1+\frac{1}{2}}x^{1+\frac{1}{2}} - \frac{x^3}{3}|_{0}^1 = \frac{2}{3}x^{\frac{3}{2}} - \frac{x^3}{3}|_{0}^1 = $$$$ = \frac{2}{3} - \frac{1}{3} = \frac{1}{3}$$
Ответ: площадь фигуры равна \(S = \frac{1}{3}\)



