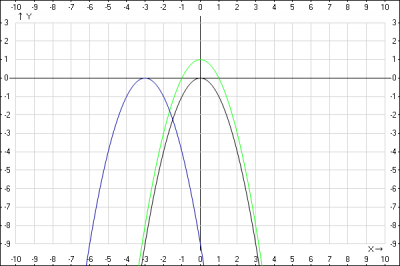
Построим графики функций:
1. \(y = -x^2\) - парабола с центром в начале координат \((0;0)\). Знак минус указываем, что оси параболы направлены вниз (цвет черный).
2. \(y = -x^2 + 1\) - парабола с центром в начале координат \((0;1)\), график функции смещен симметрично вверх вдоль оси \(Oy\) на 1. Знак минус указываем, что оси параболы направлены вниз. Найдем точки пересечения с осью \(Oy\), для этого приравняем уравнение в 0 $$-x^2 + 1 = 0 => x_1=1 \quad x_2 = -1$$ Координаты точек пересечения с осью \(Ox\) будут \((-1;0)\) и \((1;0)\) (цвет зеленый).
3. \(y = -(x+3)^2\) - парабола с центром в начале координат \((-3;0)\), график функции смещен симметрично влево вдоль оси \(Ox\) на 3. Знак минус указываем, что оси параболы направлены вниз (цвет синий).
Строим графики: