Задача: площадь основания конуса равна \(36\pi \text{ см}^2\), а его секущая равна \(10 \text{ см}\). Вычислить объем конуса.
Решение:
Объем конуса рассчитывается по формуле $$V = \frac{1}{3}S_{осн}h$$
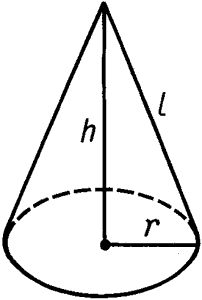
площадь основания известна \(S_{осн} = \pi r^2 = 36\pi => r = 6\). Нужно найти высоту конуса \(h\). Из рисунка видно, что по теореме Пифагора из прямоугольного треугольника получим $$ l^2 = h^2 + r^2 => h = \sqrt{l^2 - r^2} =>$$где \(h = 10\)$$h = \sqrt{10^2 - 6^2} => 8$$ Подставляем данные в формулу объема $$V = \frac{1}{3}S_{осн}h = \frac{1}{3}36\pi*8 = 96\pi$$
Ответ: объем конуса равен \(V = 96\pi\)



