Площадь поверхности сферического пояса равна \( S = 2\pi Rh \), где \( R\) - радиус сферы, \( h \) - высота сферического пояса. Таким образом, для решения задачи необходимо найти радиус сферы. Сделаем разрез сферы вдоль диаметра сферы перпендикулярного поясам сферы получим рас.
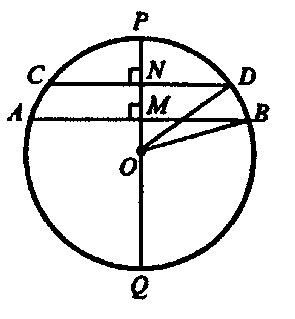
Точки пересечения поясов с диаметром обозначим \( N \), \( M \). Рассмотрим два треугольника \( ΔNDO \) и \( ΔMBO \). это два прямоугольных треугольника у которых гипотенуза - радиус сферы. Из условия задачи \( MN = 7, ND = 16, MB = 33\). Обозначим за \( x = MO\) Из теоремы Пифагора получим \( ND^2+ NO^2 = DO^2 =R^2 => ND^2 + (NM+MO)^2 = R^2 => 16^2 + (7+x)^2 = R^2 \). \( MB^2 + MO^2 = OB^2 =R^2 => 33^2 + x^2 = R^2 \).
Составим систему уравнений $$ \begin{cases}16^2 + (7+x)^2 = R^2 \\33^2 + x^2 = R^2 \end{cases} => \begin{cases} 16^2 + 49 + 14x +x^2 = 33^2 + x^2 \\ 33^2 + x^2 = R^2 \end{cases} => $$$$ \begin{cases} x = 56 \\ R^2 = 33^2 + 56^2 \end{cases} => \begin{cases} x = 56 \\ R = 65 \end{cases} $$Подставим значение радиуса в уравнение площади поверхности сферического пояса $$ S = 2\pi Rh = 2\pi 65*7 = 910 \pi$$
Ответ: площадь поверхности сферического пояса \( S = 910 \pi \, cm^2 \)



