Решение: при вращении двух синусоид вокруг оси Ox \(y=3 \sin(x); \quad y= \sin(x); \quad 0 \leq x\leq\pi \) получаем полую фигуру, смотрим рис.
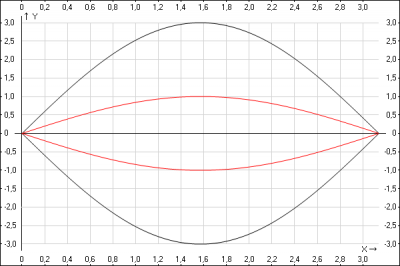
Находим объем фигуры вращения.
Объем фируры будет равен разности объемов фигур, описываемых каждой синусоидой. Рассчитаем объем фигуры вращения вокруг оси Ox по формуле $$V_x = \pi \int_a^b y_1^2dx - \pi \int_a^b y_2^2 dx$$ где \(a = 0\), \(b= \pi \), \( y_1 = 3\sin(x); \quad y_2 = \sin(x) \). Подставляем данные в формулу $$V_x = \pi \int_0^{\pi}( (3\sin(x))^2 - \sin^2(x))dx = 8\pi \int_0^{\pi} \sin^2(x)dx =$$ применим формулу косинуса двойного угла \( \cos(2x) = 1 - 2\sin^2(x) => \sin^2(x) = \frac{1 - \cos(2x)}{2}\), подставляем $$ = 4\pi \int_0^{\pi}( 1 - \cos(2x))dx = 4\pi (x - \frac{1}{2} \sin(2x))|_0^{\pi} = 4\pi^2$$
Ответ: объем фигуры вращения равен \(V_x = 4\pi^2 \)



