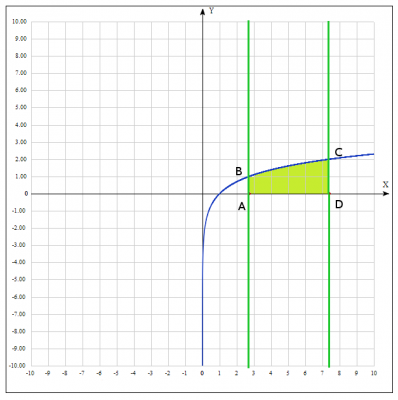
Решение: найдем площадь фигуры, ограниченную линиями \( y= \ln(x)\); \(x = e\); \(x = e^2\); \( y = 0 \)
Строим кривые:
1. \( y= \ln(x) \) - логарифмическая функция.
2. \( x = e \) - уравнение прямой, параллельной оси Oy , проходящей через точку \( x = e \)
3. \( x = e^2 \) - уравнение прямой, параллельной оси Oy , проходящей через точку \( x = e^2 \)
4. \( y = 0 \) - ось Ox.
Строим рисунок:
Нужно найти площадь криволинейной фигуры \(ABCD\)
Вспомним геометрический смысл определенного интеграла: если \(f(x) \geq 0 \) на отрезке \([a;b]\), \(a < b\), то определенный интеграл \( \int_a^bf(x)dx\) равен площади криволинейной трапеции - фигуры ограниченной линиями \(y = f(x)\), \(y = 0\), \(x=a\), \(x=b\)
Согласно условия задачи \(y = \ln(x) \), \(a = e;\quad b=e^2\) тогда искомая площадь фигуры \(ABCD\) равна $$S_{ABCD} = \int_e^{e^2}\ln(x)dx $$
Найдем неопределенный интеграл \( \int_e^{e^2}\ln(x)dx\)
Для нахождения определенного интеграла применим формулу интегрирования по частям \( \int udv = uv - \int vdu\).
Введем обозначения \( u = \ln(x) => du = \frac{1}{x}dx\), \(dv = dx => v=x\). Подставляем в формулу \( \int_e^{e^2}\ln(x)dx = x\ln(x) - \int x\frac{1}{x} dx = x\ln(x) - x + C\)
Для нахождения определенного интеграла, применим формулу Ньютона-Лейбница \(\int_a^bf(x)dx = F(x)|_a^b = F(b) - F(a)\), где \(F(x)\) мы уже нашли \(F(x) = x\ln(x) - x\),получаем $$ S_{ABCD} = \int_e^{e^2}\ln(x)dx = x\ln(x) - x|_e^{e^2} = $$$$ = e^2\ln(e^2) - e^2 - (e\ln(e) - e) = e^2$$
Ответ: площадь фигуры, которая ограничена линиями \( y= \ln(x)\); \(x = e\); \(x = e^2\); \( y = 0 \) равна \(S_{ABCD} = e^2\)



