Решение: введем следующие обозначения пусть \(A\) - точка, поставленная наугад, попала в треугольник. Для решения воспользуемся формулой геометрической вероятности $$P(A) = \frac{S_{треуг}}{S_{круг}} \quad (1)$$
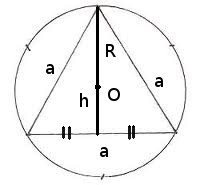
Площадь круга равна \(S_{круг} = \pi*R^2\).
Площадь вписанного в круг равностороннего треугольника будем искать по формуле \(S_{треуг} = \frac{1}{2}a*h\), где \(a\) - сторона равностороннего треугольника, \(h\) - высота треугольника. Выразим эти величины через радиус описанной окружности. Как известно высота, медиана и биссектриса в равностороннем треугольнике совпадают и пересекаются в одной точке, которая является центром описанной окружности. Найдем высоту \(h = \sqrt{a^2 - (\frac{1}{2}a)^2} = \sqrt{\frac{3}{4}}a\). В точке пересечения высоты равностороннего треугольника делятся в пропорции \(2:1\) => \(R = \frac{2}{3}h = \frac{2}{3}\sqrt{\frac{3}{4}}a = \frac{1}{\sqrt{3}}a\) => \(a = \sqrt{3}R\). Подставляем в формулу площади треугольника $$S_{треуг} = \frac{1}{2}a*h = \frac{1}{2}a*\sqrt{\frac{3}{4}}a => $$$$S_{треуг} = \frac{1}{2}*\sqrt{\frac{3}{4}}(\sqrt{3}R)^2 => $$$$ S_{треуг} = \frac{3\sqrt{3}}{4}R^2$$ Подставляем в формулу геометрической вероятности $$P(A) = \frac{S_{треуг}}{S_{круг}} = \frac{\frac{3\sqrt{3}}{4}R^2}{\pi R^2} = > $$$$ P(A) = \frac{3\sqrt{3}}{4\pi} \approx 0,413$$
Ответ: вероятность попадания точки в треугольник равна \( P(A) \approx 0,413 \)



