а) Найдем значение постоянной \(C\) функции плотности распределения \(f(x)\). Для того, чтобы функция \(f(x)\) была плотностью распределения вероятностей случайной величины \(x\) константа \(C\) должна быть \(C \geq 0\). Для нахождения значения константы воспользуемся условием \( \int_{ \alpha}^{ \beta} f(x) = 1\), подставляем данные задачи: $$ \int_{0}^{ \sqrt{3}}{ \frac{C}{(1+x^2)}} =1 => C *arctg(x)|_{0}^{ \sqrt{3}} = 1 =>$$$$C \frac{ \pi}{3} = 1 => C = \frac{3}{ \pi}$$Подставляем в формулу плотности распределения на интервале \((0; \sqrt{3})\), получаем \(f(x) = \frac{3}{\pi(1+x^2)} \)
Ответ: постоянная \(C = \frac{3}{ \pi}\), а функция распределения на интервале \((0; \sqrt{3})\) равна \(f(x) = \frac{3}{\pi(1+x^2)} \)
б) Найдем функцию распределения \(F(x)\). Для решения задачи воспользуемся формулой \( \int_{-\infty}^{x}f(t)dt = F(x)\). Найдем функцию распределения на интервалах
\( x \leq 0 \) $$ F(x) = \int_{-\infty}^{x}f(t)dt = \int_{-\infty}^{x}0dt = 0$$
\( 0 < x \leq \sqrt{3} \) $$ F(x) = \int_{-\infty}^{x}f(t)dt = \int_{-\infty}^{0}f(t)dt + \int_{0}^{ x}f(t)dt = $$$$ = \int_{-\infty}^{0}0dt + \int_{0}^{ x}\frac{3}{\pi(1+t^2)}dt = 0 + \frac{3}{ \pi} arctg(x) = \frac{3}{ \pi} arctg(x) $$
\( \sqrt{3} < x \) $$ F(x) = \int_{-\infty}^{x}f(t)dt = \int_{-\infty}^{0}f(t)dt + \int_{0}^{ \sqrt{3}}f(t)dt + \int_{ \sqrt{3}}^{ x}f(t)dt = $$$$ = \int_{-\infty}^{0}0dt + \int_{0}^{ \sqrt{3}}\frac{3}{\pi(1+t^2)}dt + \int_{ \sqrt{3}}^{x}0dt = $$$$ = 0 + \frac{3}{ \pi} arctg( \sqrt{3}) + 0 = $$$$ = 0 + \frac{3}{ \pi} \frac{ \pi}{3} +0 = 1$$
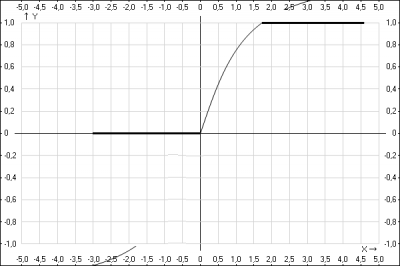
Ответ: функция распределения имеет вид: $$ F(x) = \begin{cases}0 & x \leq 0\\ \frac{3}{ \pi} arctg(x) & 0 < x \leq \sqrt{3}\\ \\ 1 & \sqrt{3} < x \end{cases} $$
в) Найдем математическое ожидание \(M(x)\)
Математическим ожиданием непрерывной случайной величины \(X\), возможные значения которой принадлежат отрезку \([a;b]\) находится по формуле $$M(x) = \int_{a}^{b}xf(x)dx$$Математическое ожидание равно $$M(x) = \int_{0}^{\sqrt{3}}\frac{3x}{\pi(1+x^2)}dx = $$ введем замену \(t^2 = 1+x^2 => 2tdt = 2xdx => tdt = xdx\), получаем \( \int \frac{3t}{\pi t^2}dt = \int \frac{3}{ \pi t}dt = \frac{3}{ \pi}\ln(t) = \) применяем обратную замену \( = \frac{3}{ \pi} \ln(\sqrt{1+x^2})\). Подставляем в формулу математического ожидания $$ = \frac{3}{ \pi} \ln(\sqrt{1+x^2})|_{0}^{\sqrt{3}} = \frac{3}{ \pi} \ln(\sqrt{1+( \sqrt{3})^2}) - \frac{3}{ \pi} \ln(\sqrt{1+0^2}) =$$$$ = \frac{3}{ \pi} \ln(\sqrt{1+3}) = \frac{3}{ \pi} \ln(\sqrt{4}) = \frac{3}{ \pi}\ln(2) \approx 0,662$$
Ответ: математическое ожидание равно \(M(x) = 0,662\)
г) Найдем дисперсию \(D(x)\)
Дисперсию непрерывной случайной величины будем искать по формуле \(D(x) = \int_{ \alpha}^{ \beta}(x - M(x))^2f(x)dx\). Подставляем исходные данные в формулу дисперсии$$D(x) = \int_{ 0}^{ \sqrt{3}}(x - \frac{3}{ \pi}\ln(2))^2\frac{3}{\pi(1+x^2)}dx = $$$$ =\frac{3}{\pi}(\int_{ 0}^{ \sqrt{3}}\frac{x^2}{1+x^2}dx - 2\int_{ 0}^{ \sqrt{3}}\frac{x \frac{3}{ \pi}\ln(2)}{1+x^2}dx + \int_{ 0}^{ \sqrt{3}}(\frac{3}{ \pi}\ln(2))^2\frac{1}{1+x^2}dx) =$$$$ = \frac{3}{\pi}(x - arctg(x)|_{0}^{\sqrt{3}} - \frac{6}{ \pi}\ln(2) \ln(\sqrt{1+x^2})|_{0}^{\sqrt{3}} + (\frac{3}{ \pi}\ln(2))^2arctg(x)|_{0}^{\sqrt{3}}) = $$$$ = \frac{3}{\pi}( \sqrt{3} - arctg( \sqrt{3}) - \frac{6}{ \pi}\ln(2) \ln(\sqrt{1+(\sqrt{3})^2}) + (\frac{3}{ \pi}\ln(2))^2arctg( \sqrt{3})) =$$$$ = \frac{3}{\pi}( \sqrt{3} - \frac{ \pi}{3} - \frac{6}{ \pi}\ln^2(2) + (\frac{3}{ \pi}\ln(2))^2\frac{ \pi}{3}) \approx 0,216 $$
Ответ: математическое ожидание равно \(D(x) = 0,216\)
д) Найдем среднеквадратическое отклонение \( \sigma_x\)
Среднеквадратическое отклонение будем искать по формуле \( \sigma_x = \sqrt{D(x)}\) $$\sigma_x = \sqrt{0,216} = 0.465 $$
е) Найдем вероятность \(P(x > M(x))\)
Вероятность попадания значений случайной величины \(X\) в интервал \(( \alpha; \beta)\) равна \(P( \alpha < x < \beta) = \int_{ \alpha}^{ \beta}f(x)dx \). Подставляем исходные данные в формулу вероятности $$ P( 0,662 < x < \sqrt{3}) = \int_{ 0,662}^{ \sqrt{3}}\frac{3}{\pi(1+x^2)}dx = \frac{3}{ \pi} arctg(x)|_{ 0,662}^{ \sqrt{3}} = \frac{3}{ \pi} ( arctg(\sqrt{3}) - arctg(0,662)) = \frac{1}{2} $$
График функции плотности распределения \(f(x)\)
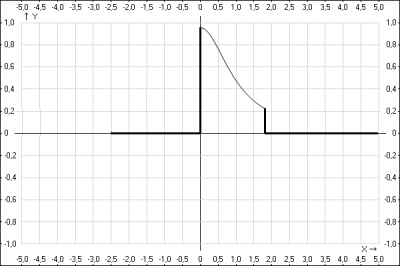
График функции распределения \(F(x)\)