Дано: уравнение кривой в полярной системе координат \( \rho = a(1 + \cos(\phi))\) .
построим кривую по точкам, путем составления таблицы значений функции
Решение:
Составим таблицу значений функции, при этом будем считать параметр \(a = 1\), получим
$$\begin{array}{|c|c|c|с|c|}
\hline \\ \phi & 0&\frac{\pi}{4} & \frac{\pi}{2} & \frac{3\pi}{4} & \pi & \frac{5\pi}{4} & \frac{3\pi}{2} & \frac{7\pi}{4} & 2\pi \\
\hline \\ \rho (a=1) & 2 & 1,71 & 1 & 0,29 &0 & 0,29 & 1 & 1,71 &2\\ \hline
\hline \\ x( \rho*\cos(\phi)) & 2 & 1,2 & 0 & -0,21 &0 & -0,21 & 0 & 1,2 &2 \\ \hline
\hline \\ y( \rho*\sin(\phi)) & 0 & 1,2 & 1 & 0,21 &0 & -0,21 & -1 & -1,2 &0 \\ \hline
\end{array}$$
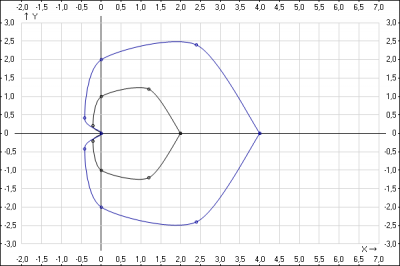
По этим данным отметим точки на плоскости и, плавно соединяя соседние точки, построим линию.
Аналогично построим и для параметра \(a=2\)
$$\begin{array}{|c|c|c|с|c|}
\hline \\ \phi & 0&\frac{\pi}{4} & \frac{\pi}{2} & \frac{3\pi}{4} & \pi & \frac{5\pi}{4} & \frac{3\pi}{2} & \frac{7\pi}{4} & 2\pi \\
\hline \\ \rho (a=2) & 4 & 3,42 & 2 & 0,58 &0 & 0,58 & 2 & 3,42 & 4 \\ \hline
\hline \\ x( \rho*\cos(\phi)) & 4 & 2,4 & 0 & -0,42 &0 & -0,42 & 0 & 2,4 &4 \\ \hline
\hline \\ y( \rho*\sin(\phi)) & 0 & 2,4 & 2 & 0,42 &0 & -0,42 & -2 & -2,4 &0 \\ \hline
\end{array}$$
По этим данным отметим точки на плоскости и, плавно соединяя соседние точки, построим линию.
Аналогично можно построить кривую при любом параметре \(a\)
Получили семейство кривых, которое нанесем на декартовую систему координат