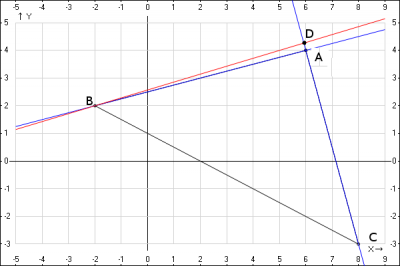
Заданы вершины треугольника A(6,4); B(-2,2); C(8,-3). Найти уравнение стороны AB, уравнение высоты BD.
1. Уравнения сторон треугольника.
Даны три вершины треугольника, поэтому уравнения сторон будем искать ка уравнение прямой , проходящей через две заданные точки \( \frac{x-x_1}{x_2-x_1} = \frac{y-y_1}{y_2-y_1} \quad (1) \) Подставляем координаты вершин:
уравнение стороны AB, при известных координатах вершины A(6;4) и B(-2;2) $$AB \quad \frac{x-6}{-2-6} = \frac{y-4}{2-4} => y = \frac{x}{4}+\frac{5}{2}$$
2. Уравнение высоты BD.
Высота BD опущена из вершины B на сторону AC. Из условия задачи известна одна координата точки B(-2;2) и направление - прямая BD перпендикулярна прямой AC. Воспользуемся свойством угловых коэффициентов перпендикулярных прямых: \(k_1 = -\frac{1}{k_2}\). Найдем угловой коэффициент \(k_{BD} = -\frac{1}{k_{AC}} \).
Найдем уравнение прямой AC для этого воспользуемся уравнением прямой проходящей через две заданные точки A(6;4) и C(8;-3) $$AC \quad \frac{x-6}{8-6} = \frac{y-4}{-3-4} => y = -\frac{7}{2}x + 25$$ Получили угловой коэффициент \(k_{AC} = -\frac{7}{2} \) т.к. $$k_{BD} = -\frac{1}{k_{AC}} = \frac{2}{7}$$ Получили угловой коэффициент прямой BD, уравнение прямой найдем воспользовавшись уравнением прямой, проходящей через заданную точку в заданном направлении в заданном направлении \( y-y_1 = k_1(x-x_1)\), получим $$ y - 2 = \frac{2}{7}(x + 2) => y = \frac{2}{7}x + \frac{18}{7}$$
3. Наносим на декартовую систему координат полученные уравнения и координаты точек.