Вычислить площадь плоской фигуры, ограниченной заданными кривыми. Сделать чертеж области.

Найдем площадь фигуры, ограниченную кривыми $y=x^3+2; \quad x=0 \quad y=x+6 \quad x = -2$.
1. Сделаем чертеж, на чертеже обозначим фигуру, площадь которой требуется найти.

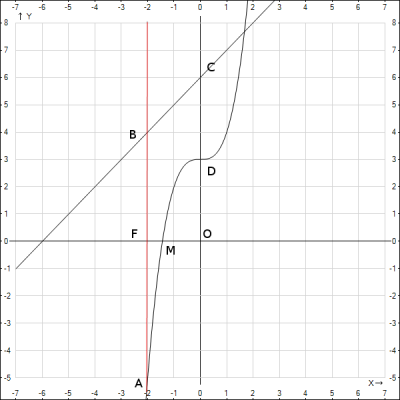
2. Найдем площадь фигуры $ABCD$.
Фигура, ограниченная заданными кривыми - $ABCD$.
Из рисунка видно, что $$S_{ABCD} = S_{FBCDM} + S_{AFM}$$
В то же время $$S_{FBCDM} =  S_{FBCO} -  S_{MDO}$$ где FBCO - прямоугольная трапеция, т.е. окончательно получим $$S_{ABCD} = S_{FBCO} -  S_{MDO} + S_{AFM} = S_{FBCO} -  (S_{MDO} - S_{AFM})$$
Найдем площадь прямоугольной трапеции FBCO по формуле площади трапеции $S_{трап} = \frac{a+b}{2}h$.
Найдем основания и высоту трапеции
основание $a = FB = 4$ - равно ординате (y) точки пересечения прямых $x = -2$ и (y=x+6), т.е. $y = -2 + 6 = 4$
основание $b = OC = 6$ - равно ординате (y) точки пересечения прямой (y=x+6) и оси Oy,т.е. $y = 0 + 6 = 6$
высота $h = FO = 2$
тогда площадь трапеции равна $$S_{FBCO} = \frac{4+6}{2}*2=10$$
Найдем площадь $S =  S_{MDO} - S_{AFM}$.
Для нахождения этих площадей воспользуемся геометрическим смыслом определенного интеграла - интеграл равен площади фигуры, ограниченной графиком функции $y = x^3+2$, осью y = 0, прямыми x = 0 и x = -2.
Нужно учесть, что значение определенного интеграла над осью Ox  будет дольше 0 , а значение под осью Ox будет меньше 0, т.е. интеграл нам даст $S = S_{MDO} - S_{AFM}$, а это нам и нужно, т.е. в данном случае нет необходимости находить координату точки M и искать два определенных интеграла от функции $y = x^3+2$ на отрезках FM и MO, а затем их  вычитать  $$\int_{-2}^0 (x^3+2)dx = \frac{1}{4}x^4+2x|_{-2}^0 = 0 - (\frac{1}{4}(-2)^4+2(-2)) = -4+4=0$$ Это означает, что $S_{MDO} = S_{AFM}$.
Окончательно получаем $$S_{ABCD} = S_{FBCO} = 10$$