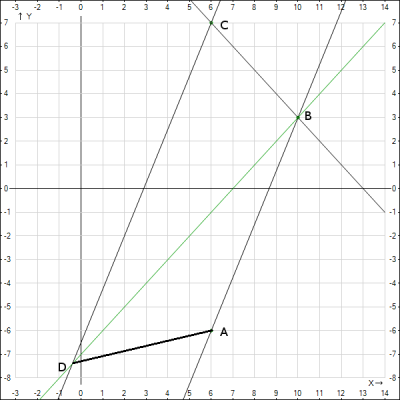
1) длину стороны АВ.
Длину стороны AB будем искать по формуле расстояния между точками $$d = \sqrt{ (x_2-x_1)^2 + (y_2-y_1)^2}$$ Подставляем координаты точек А(6;-6) В(10;3), получаем $$AB = \sqrt{ (10-6)^2 + (3+6)^2} = \sqrt{97} \approx 9,85$$
2) уравнение прямой АВ.
Уравнения прямой будем искать как уравнение прямой, проходящей через две заданные точки $$ \frac{x-x_1}{x_2-x_1} = \frac{y-y_1}{y_2-y_1}$$ Подставляем координаты точек А(6;-6), В(10;3) и получаем уравнение прямой $$ \frac{x-6}{10-6} = \frac{y+6}{3+6} => y = \frac{9}{4}x - \frac{39}{2}$$
3) уравнение прямой BC.
Уравнения прямой будем искать как уравнение прямой, проходящей через две заданные точки $$ \frac{x-x_1}{x_2-x_1} = \frac{y-y_1}{y_2-y_1}$$ Подставляем координаты точек В(10;3), С(6;7) и получаем уравнение прямой $$ \frac{x-10}{6-10} = \frac{y-3}{7-3} => y = -x + 13$$
4) уравнение прямой CD.
О прямой CD известно, что она параллельна (прямой) AB. Воспользуемся свойством параллельных прямых: угловые коэффициенты параллельных прямых равны \(k_{AB}=k_{CD} = \frac{9}{4}\). Для прямой CD известен угловой коэффициент и точка, через которую она проходит. Воспользуемся уравнением прямой, проходящей через заданную точку в заданном направлении $$y - y_0 = k(x-x_0)$$Подставляем координаты точки С(6;7) и угловой коэффициент \(k_{CD} = 1\) $$y - 7 = \frac{9}{4}(x-6) => y = \frac{9}{4}x -\frac{13}{2}$$
5) величину угла \(\widehat{BCD}\).
Известны уравнения прямых, образующих угол \( \widehat{BCD} \) - прямые BC и CD. Угол между прямыми ищется по формуле $$ tg \phi = | \frac{k_2-k_1}{1+k_2k_1}|$$ Угловые коэффициенты прямых равны \(k_{BC} = -1\), \(k_{CD} = \frac{9}{4}\), подставляем в формулу $$ tg \phi = | \frac{ \frac{9}{4}+1}{1+\frac{9}{4}(-1)}| = \frac{13}{4}\frac{4}{5} = \frac{13}{5} \approx 69^0$$
6) высоту трапеции.
Высоту трапеции будем рассматривать ка расстояние от точки до прямой - расстояние одной из вершин, например А(6;-6) до прямой CD. Расстояние (высоту) будем искать по формуле $$h = |\frac{Ax_0+By_0+C}{ \sqrt{A^2+B^2}}|$$ где \( Ax+By+C =0\) - уравнение прямой, а \( x_0;y_0\) - координаты точки. Представим уравнение прямой CD в общем виде \(y = \frac{9}{4}x -\frac{13}{2} => 4y -9x+26 =0\). Подставим полученное уравнение прямой координаты точки А(6;-6) в формулу $$h = |\frac{4*(-6) -9*6+26}{ \sqrt{6^2+6^2}}| = \frac{52}{\sqrt{72}} = \frac{26}{3 \sqrt{2}} \approx 6,13$$
7) Нанесем координаты точек и прямых на декартовую систему координат.