Ищем координаты вершин ромба. Предварительно определим, уравнения каких сторон (параллельных или пересекающихся). Т.у. коэффициенты при неизвестных двух прямых пропорциональные с коэффициентом один (т.е. равны) это означает, что прямые параллельные, а в пересечении с диагональю получим две координаты вершин A(x;y) и B(x;y)
1. Координаты первой вершины A.
Найдем точку пересечения диагонали и одной из прямых - первая вершина ромба. Составим систему уравнений и найдем эти координаты $$\begin{cases}х+2у-4=0 \\у=х+2\end{cases} => \begin{cases}х+2у-4=0 \\у-х-2=0\end{cases} => $$$$ \begin{cases}3у-6=0 \\ у-х-2=0\end{cases} => \begin{cases}у=2 \\х=0\end{cases}$$Координаты вершины \(A(0;2)\)
2. Координаты первой вершины B.
Найдем точку пересечения диагонали и второй прямой - вторая вершина ромба. Составим систему уравнений и найдем эти координаты $$\begin{cases}х+2у-10=0 \\у=х+2\end{cases} => \begin{cases}х+2у-10=0 \\ у-х-2=0\end{cases} => $$$$ \begin{cases}3у-12=0 \\у-х-2=0\end{cases} => \begin{cases}у=4 \\х=2\end{cases}$$Координаты вершины \(B(2;4)\)
3. Уравнение диагонали CD.
Найдем уравнение второй диагонали, а затем координаты оставшихся точек по аналогии как в п.1,2.
Воспользуемся свойством угловых коэффициентов двух перпендикулярных прямых \( k_1 = -\frac{1}{k_2} \). Угловой коэффициент диагонали AB \(у=х+2 =>\) \( k =1 =>\) Угловой коэффициент диагонали CD \(k_{CD} = - \frac{1}{1} = -1\) .Зная угловой коэффициент и одну точку, через которую проходит прямая диагонали, уравнение найдем по формуле уравнения прямой, проходящей через заданную точку в заданном направлении $$y - y_0 = k(x-x_0) \quad (1)$$Точка, через которую проходит диагональ \(CD\) - середина диагонали \(AB\) это следует из свойства диагоналей ромба. Находим координаты точки O - середины диагонали \(AB\) \(O( \frac{x_A+x_B}{2}; \frac{y_A+y_B}{2}) => O( \frac{0+2}{2}; \frac{2+4}{2})\) Координаты точки пересечения диагоналей \(O(1;3)\). Подставляем координаты точки и углового коэффициента в (1) $$y - 3 = -(x-1) => y = -x + 4$$
4. Координаты первой вершины C.
Найдем точку пересечения диагонали и второй прямой - вторая вершина ромба. Составим систему уравнений и найдем эти координаты $$\begin{cases}х+2у-10=0 \\у=-х+4\end{cases} => \begin{cases}х+2у-10=0 \\у+х-4=0\end{cases} => \begin{cases}у=6 \\х=-2\end{cases}$$ Координаты вершины C(-2;6)
5. Координаты первой вершины D.
Найдем точку пересечения диагонали и второй прямой - вторая вершина ромба. Составим систему уравнений и найдем эти координаты $$\begin{cases}х+2у-4=0 \\у=-х+4\end{cases} => \begin{cases}х+2у-4=0 \\у+х-4=0\end{cases} => \begin{cases}у=0 \\х=4\end{cases}$$ Координаты вершины D(4;0)
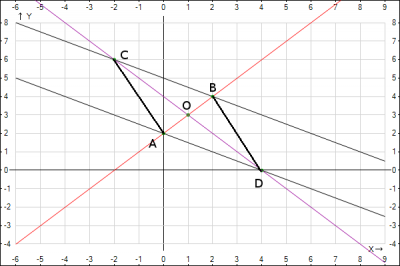
6. Наносим на декартовую систему координат полученные результаты.