Найдем напряженность электрического поля, создаваемого бесконечной заряженной нитью с известной линейной плотностью заряда \(\tau=10^{12}\frac{Кл}{м}\) на расстоянии \(l=20см\).
Согласно теореме Гаусса: поток вектора напряженности \(\vec{E}\) через произвольную замкнутую поверхность равен алгебраической сумме зарядов, заключенных внутри этой поверхности, деленной на \(ε_0\) (ε0 - электрическая постоянная) $$\phi = \frac{\sum q}{\epsilon_0} \quad (1)$$ С другой стороны, согласно определения
поток вектора напряженности равен \(\phi = \vec{E}*S_{пов} \quad (2)\), приравняем обе формулы (1) и (2), получим $$ \vec{E}*S_{пов}= \frac{\sum q}{\epsilon_0} =>\vec{E} = \frac{\sum q}{S_{пов}\epsilon_0} \quad (3)$$Т.е. для решения данной задачи нужно найти саму поверхность (ее площадь) и суммарный заряд, заключенный в этой поверхности.
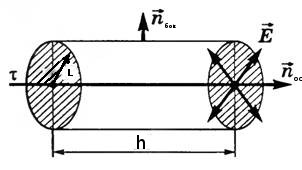
1.Поверхность. Поверхностью, в которой находится заряд будет цилиндр с осью - сама нить, радиусом основания равным \(r = l = 30см\) и высотой \(h\). Согласно определения потока \(\phi = \vec{E}*S_{пов} =>\phi = E*S_{пов} \cos \alpha\) , где \( \alpha\) - угол между вектором напряженность и нормальным вектором к поверхности. Т.е поток через наш цилиндр будет равен $$\phi = \phi_{осн} + \phi_{бок}$$ Вектор напряженности будет перпендикулярен боковой поверхности, т.е. он параллелен нормальному вектору поверхности \(\vec{n_{бок}}\), тогда \(\cos \alpha = \cos 0^0=1 =>\) \(\phi = E*S_{бок}\), в тоже время вектор напряженности перпендикулярен нормальному вектору основания цилиндра \(\vec{n_{осн}}\), т.е. \(\cos \alpha = \cos 90^0= 0 =>\) \(\phi = E*S_{осн} =0\). Получили $$\phi = \phi_{бок} = E*S_{бок}$$Т.е нам необходимо найти площадь боковой поверхности цилиндра, которая равна \(S_{бок} =2\pi r*h\), где r - радиус основания цилиндра и он равен расстоянию до точки \(r = l =>S_{бок} =2\pi l*h\)
2. Заряд. Найдем алгебраическую сумму зарядов внутри цилиндра. Высота цилиндра равна \(h\). Плотность распределения заряда известна - они линейная и равна \(\tau\), тогда суммарный заряд будет равен \(\sum q = h*\tau\).
Подставляем, полученные данные в формулу (3), получаем $$E = \frac{\sum q}{S_{бок}\epsilon_0} = \frac{ h*\tau}{2\pi r*h\epsilon_0} = \frac{\tau}{2\pi r\epsilon_0}$$Получили формулу для вектора напряженности, подставляем данные задачи, предварительно переведем все данные в систему единиц СИ \( \tau=10^{-12} \frac{Кл}{м} \)$$ E=\frac{10^{-12}\frac{Кл}{м}}{2\pi 0,2 м 8,85*10^{-12}\frac{Ф}{м}}=9*10^{-2}\frac{Кл}{Фм}=9*10^{-2}\frac{Кл}{\frac{Кл}{В}м} => $$$$ E=9*10^{-2}\frac{В}{м} $$



