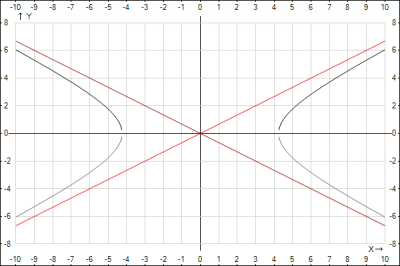
Каноническое уравнение гиперболы $$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$$ Для того, чтобы построить гиперболу найдем ее полуоси. В условии даны уравнения асимптот, запишем общее уравнение асимптот гиперболы \(y = \pm \frac{b}{a}x\), согласно условия задачи $$ \pm \frac{b}{a}x = \pm \frac{2}{3}x => \frac{b}{a} = \frac{2}{3}$$ получили первое уравнение, связывающее мнимую и действительную полуоси.
Второе уравнение получим, подставив в каноническое уравнение координаты известной точки\( М(\frac{9}{2};-1)\), получим \(\frac{(\frac{9}{2})^2}{a^2}-\frac{(1)^2}{b^2}=1\). Объединим полученные уравнения в систему уравнения из двух переменных и решим ее $$\begin{cases}\frac{(\frac{9}{2})^2}{a^2}-\frac{(1)^2}{b^2}=1\\ \frac{b}{a} = \frac{2}{3} \end{cases} => \begin{cases}\frac{81}{4a^2}-\frac{1}{b^2}=1\\ b = \frac{2}{3}a \end{cases} => $$$$ \begin{cases}\frac{81}{4a^2}-\frac{1}{(\frac{2}{3}a)^2}=1\\ b = \frac{2}{3}a \end{cases} => \begin{cases}\frac{81}{4a^2}-\frac{9}{4a^2}=1\\ b = \frac{2}{3}a \end{cases} => $$$$ \begin{cases}\frac{72}{4a^2}=1\\ b = \frac{2}{3}a \end{cases} => \begin{cases}a= 3\sqrt{2}\\ b = 2\sqrt{2} \end{cases}$$Подставляем значения полуосей в уравнение гиперболы $$\frac{x^2}{18}-\frac{y^2}{8}=1$$
Наносим на декартовую систему координат гиперболу и асимптоты.