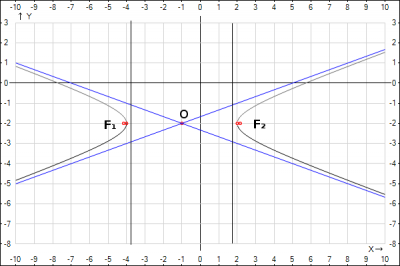
Дано уравнение кривой второго порядка \(x^2-9y^2+2x-36y-44=0\)
1. Записать уравнение кривой в каноническом виде.
В данном уравнении есть только члены второй и первой степени (нет смешанного произведения), поэтому каноническое уравнение будем получать методом выделения полного квадрата.
$$x^2-9y^2+2x-36y-44=0 => x^2+2x-9y^2-36y-44=0 $$$$ (x^2+2x)-9(y^2+4y)-44=0=> (x^2+2*1*x+1-1)-9(y^2+2*2y+4-4)-44=0 =>$$$$ (x+1)^2-1-9(y+2)^2+36-44=0 => (x+1)^2-9(y+2)^2 =9 =>$$осталось последнее действие - разделим обе части уравнения на$$= \frac{(x+1)^2}{9}-\frac{(y+2)^2}{1} =1$$Получили уравнение гиперболы. Каноническое уравнение гиперболы $$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$$Для того, чтобы привести к указанному виду введем новые координаты \(x'=x+1;y'=y+2\), подставляем и получаем каноническое уравнение в новой системе координат, которая смещена относительно первичной системы координат на по оси Ох влево на 1 и по оси Оу на 2 вниз, получаем $$\frac{(x')^2}{9}-\frac{(y')^2}{1}=1$$При этом действительная ось лежит на оси Ox, действительная полуось равна\(a =3\) , а мнимая на ось Oy, мнимая полуось равна \(b = 1\).
2. Найти координаты фокусов, вершин, центр.
Рассмотрим полученное уравнение гиперболы. \( \frac{(x+1)^2}{9}-\frac{(y+2)^2}{1} =1\) .
Точка пересечения осей симметрии - центр гиперболы. Координаты центра \(O(-1;-2)\)
Точки пересечения с осью, в данном случае с осью Ox - вершины гиперболы, т.е. при y=-2 $$\frac{(x+1)^2}{9} = 1 => x = \pm3 -1$$, т.е. координаты вершины равны $$A_1(-4; -2); A_2(2; -2)$$ Координаты фокусов гиперболы с центром в начале координат (x';y') равны \(F_1(0;c);F_2(0;-c)\), где фокусное расстояние находятся по формуле \(c^2=a^2+b^2\) подставляем значения полуосей и получаем $$c = \sqrt{9+1} = \sqrt{10}$$ т.к. по условию задачи центра смещен \(x'=x+1;y'=y+2\) => \(x=x'-1;y=y'-2\) координаты фокусов будут равны \(F_1(-c-1;-2);F_2(-c-1;-2)\) , т.е. координаты фокусов в первичной системе координат равны \(F_1(-\sqrt{10}-1;-2);F_2(\sqrt{10}-1;-2)\)
3.Записать уравнение директрис и асимптот
Асимптоты. Уравнения асимптот равны \(y'= \pm \frac{b}{a}x\), с учетом сдвига системы координат \(y+2 = \pm \frac{1}{3}(x+1) => y = \pm \frac{1}{3}(x+1) -2\) Получили два уравнения асимптоты $$y = -\frac{1}{3}x -\frac{7}{3}$$ и $$y = \frac{1}{3}x - \frac{5}{3}$$
Уравнение директрисы для системы координат \(x';y'\) находится по формуле \(x' = \pm \frac{a}{\epsilon} = \pm \frac{a}{\frac{c}{a}} = \pm \frac{a^2}{c}\) С учетом сдвига получаем $$x+1= \pm \frac{9}{\sqrt{10}} =>$$первое уравнение директрисы $$x = \frac{9}{\sqrt{10}}-1 \approx 1,85$$второе уравнение директрисы $$x = -\frac{9}{\sqrt{10}}-1 \approx -3,85$$
4. Построить рисунок: