Схема решения задачи следующая.
1. Находим уравнение медианы.
2. Зная уравнение медианы, ищем расстояние от точки до прямой (медианы) это и будет длина перпендикуляра.
Решение:
1. Найдем уравнение медианы, опущенной из вершины C.
Уравнение медианы будем искать по формуле уравнения прямой, проходящей через две заданные точки $$\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1} \quad (1)$$ Одна точка для уравнения есть С (2,1), координаты второй точки M получим как середину между точками А(-10,-13), В(-2,3) $$M(\frac{x_A+x_B}{2}; \frac{y_A+y_B}{2}) =>$$ подставляем координаты точек $$M(\frac{-10-2}{2}; \frac{-13+3}{2}) => M(-6; -5)$$Получили координаты второй точки, подставляем в уравнение прямой (1) $$\frac{x-2}{-6-2}=\frac{y-1}{-5-1} => y = \frac{3}{4}x - \frac{1}{2}$$
2. Найдем расстояние отточки до прямой.
Уравнение прямой, расстояние до которой нужно найти $$y = \frac{3}{4}x - \frac{1}{2} => 4y -3x+2=0$$ Координаты точки В(-2,3). Расстояние от точки до прямой рассчитываются по формуле $$d= \frac{Ax_0+By_0+C}{\sqrt{A^2+b^2}}$$где \((x_0;y_0)\) - координаты точки C, \(Ax_0+By_0+C\) - уравнение медианы , подставляем координаты и получаем $$d= \frac{4*3 -3*(-2)+2}{ \sqrt{4^2+3^2}} = \frac{20}{5} = 4$$
3. Наносим точки и прямые на координатную плоскость и проверяем правильность решения.
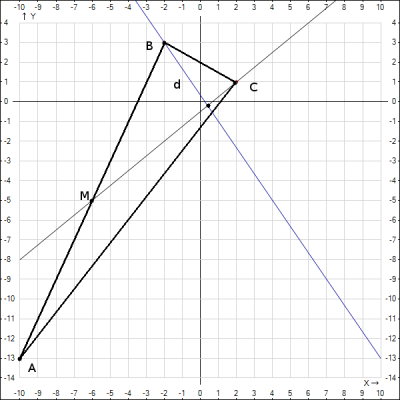
Ответ: длина перпендикуляра, опущенного из вершины D на медиану, т.е. расстояние от этой точки до прямой равно \(d=4\)



