Дано уравнение кривой второго порядка \(y^2+3x-6y+15=0\)
1. Записать уравнение кривой в каноническом виде.
В данном уравнении есть только члены второй и первой степени (нет смешанного произведения), поэтому каноническое уравнение будем получать методом выделения полного квадрата.
$$y^2+3x-6y+15=0=> y^2-6y+3x+15=0$$$$ (y^2-2*3y)+3x+15=0 => (y^2-2*3y+9-9)+3x+15=0 =>$$$$(y-3)^2-9+3x+15=0 => (y-3)^2= -3x-6 => (y-3)^2= -3(x+2)$$Получили уравнение параболы. Введем замену координат \(x'=x+2\) и \(y'=y-3\) получаем каноническое уравнение имеет вид $$ (y')^2 = -3x'$$ получили каноническое уравнение параболы, осью симметрии которой является ось Ox и оси которой направлены влево т.е. x
2. Найти координаты фокуса, вершины, параметр.
Из уравнения параболы $$(y-3)^2= -3(x+2)$$ следует, что координаты вершины равны \(M(-2;3)\) , а осью симметрии является прямая $$y - 3 =0 => y =3$$
Найдем параметр параболы, сравниваем каноническое уравнение параболы \(y^2= -2px\) и уравнение параболы в задании \((y-3)^2= -3(x+2)\) видим, что \(2p =3 => p=\frac{3}{2} \).
Фокус - точка, которая лежит на оси симметрии \(y=3\) на расстоянии \(\frac{p}{2} = \frac{\frac{3}{2}}{2} = \frac{3}{4}\) от вершины, т.е. фокус имеет координаты \(F(-2-\frac{3}{4};3)\) $$F(-\frac{11}{4};3) $$
3.Записать уравнение директрисы.
Уравнение директрисы в системе координат \(X'OY'\) имеет вид \(x' = \frac{p}{2} = \frac{3}{4}\), тогда в системе координат \(XOY\) будет иметь вид $$x+2=\frac{3}{4} => x = -\frac{5}{4}$$
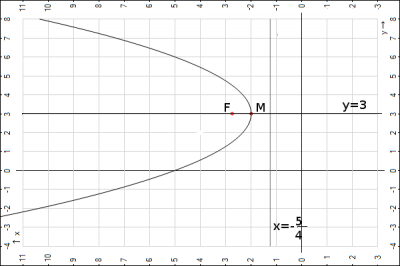
4. Построить рисунок: