1. Уравнение сторон АВ и ВС и их угловые коэффициенты.
В задании даны координаты точек, через которые проходят эти прямые, поэтому воспользуемся уравнением прямой, проходящей через две заданные точки $$\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}$$ подставляем и получаем уравнения
уравнение прямой AB $$\frac{x+6}{6+6}=\frac{y-8}{-1-8} => y = -\frac{3}{4}x + \frac{7}{2}$$ угловой коэффициент прямой AB равен \(k_{AB} = -\frac{3}{4}\)
уравнение прямой BC $$\frac{x-4}{6-4}=\frac{y-13}{-1-13} => y = -7x + 41$$ угловой коэффициент прямой BC равен \(k_{BC} = -7\)
2. Угол В в радианах с точностью до двух знаков
Угол B - угол между прямыми AB и BC, который рассчитывается по формуле $$tg\phi=|\frac{k_2-k_1}{1+k_2*k_1}|$$подставляем значения угловых коэффициентов этих прямых и получаем $$tg\phi=|\frac{-7+\frac{3}{4}}{1+7*\frac{3}{4}}| = 1 => \phi = \frac{\pi}{4} \approx 0.79$$
3.Длину стороны АВ
Длина стороны AB рассчитывается как расстояние между точками и равна \(d = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\) => $$d_{AB} = \sqrt{(6+6)^2+(-1-8)^2} = 15$$
4.Уравнение высоты CD и ее длину.
Уравнение высоты будем находить по формуле прямой проходящей через заданную точку С(4;13) в заданном направлении - перпендикулярно прямой AB по формуле \(y-y_0=k(x-x_0)\). Найдем угловой коэффициент высоты \(k_{CD}\) воспользовавшись свойством перпендикулярных прямых \(k_1=-\frac{1}{k_2}\) получим $$k_{CD}= -\frac{1}{k_{AB}} = -\frac{1}{-\frac{3}{4}} = \frac{4}{3}$$ Подставляем в уравнение прямой, получаем $$y - 13 = \frac{4}{3}(x-4) => y = \frac{4}{3}x+\frac{23}{3}$$ Длину высоты будем искать как расстояние от точки С(4;13) до прямой AB по формуле $$d = \frac{Ax_0+By_0+C}{\sqrt{A^2+B^2}}$$ в числителе уравнение прямой AB, приведем его к этому виду \(y = -\frac{3}{4}x + \frac{7}{2} => 4y+3x-14 = 0\) , подставляем полученное уравнение и координаты точки в формулу $$d = \frac{4*13+3*4-14 }{\sqrt{4^2+3^2}} = \frac{50}{5} =10$$
5. Уравнение медианы АЕ и координаты точки К пересечение этой медианы с высотой CD.
Уравнение медианы будем искать как уравнение прямой, проходящей через две заданные точки А(-6;8) и E , где точка E - середина между точками B и C и ее координаты находятся по формуле \(E(\frac{x_2+x_1}{2};\frac{y_2+y_1}{2})\) подставляем координаты точек \(E(\frac{6+4}{2};\frac{-1+13}{2})\) => \(E(5; 6)\), тогда уравнение медианы AE буде следующее $$\frac{x+6}{5+6}=\frac{y-8}{6-8} => y = -\frac{2}{11}x + \frac{76}{11}$$Найдем координаты точки пересечения высот и медианы, т.е. найдем их общую точку Для этого составим систему уравнение $$\begin{cases}y = -\frac{2}{11}x + \frac{76}{11}\\y = \frac{4}{3}x+\frac{23}{3}\end{cases}=>\begin{cases}11y = -2x +76\\3y = 4x+23\end{cases}=>$$$$\begin{cases}22y = -4x +152\\3y = 4x+23\end{cases}=> \begin{cases}25y =175\\3y = 4x+23\end{cases}=> $$$$\begin{cases}y =7\\ x=-\frac{1}{2}\end{cases}$$ Координаты точки пересечения \(K(-\frac{1}{2};7)\)
6.Уравнение прямой что проходит через точку К параллельно к стороне АВ.
Если прямая параллельны, то их угловые коэффициенты равны, т.е. \(k_{AB}=k_{K} = -\frac{3}{4}\) , также известны координаты точки \(K(-\frac{1}{2};7)\), т.е. для нахождения уравнения прямой применим формулу уравнения прямой, проходящей через заданную точку в заданном направлении \(y - y_0=k(x-x_0)\), подставляем данные и получаем $$y - 7= -\frac{3}{4}(x-\frac{1}{2}) => y = -\frac{3}{4}x + \frac{53}{8}$$
8. Координаты точки М которая симметрична точке А относительно прямой CD.
Точка M лежит на прямой AB, т.к. CD - высота к этой стороне. Найдем точку пересечения CD и AB для этого решим систему уравнений $$\begin{cases}y = \frac{4}{3}x+\frac{23}{3}\\y = -\frac{3}{4}x + \frac{7}{2}\end{cases} =>\begin{cases}3y = 4x+23\\4y =-3x + 14\end{cases} => $$$$\begin{cases}12y = 16x+92\\12y =-9x + 42\end{cases} =>
\begin{cases}0= 25x+50\\12y =-9x + 42\end{cases} => $$$$\begin{cases}x=-2\\y=5 \end{cases}$$ Координаты точки D(-2;5). По условию AD=DK, это расстояние между точками находится по формуле Пифагора \(d = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\), где AD и DK - гипотенузы равных прямоугольных треугольников, а \(Δx =x_2-x_1\) и \(Δy=y_2-y_1\) - катеты этих треугольников, т.е. найдем катеты найдем и координаты точки M. \(Δx=x_D-x_A = -2+6=4\), а \(Δy=y_D-y_A = 5-8=-3\), тогда координаты точки M будут равны \(x_M-x_D = Δx => x_D +Δx =-2+4=2 \), а \(y_M-y_D = Δy => y_D +Δy =5-3=2 \), получили, что координаты точки \(M(2;2)\)
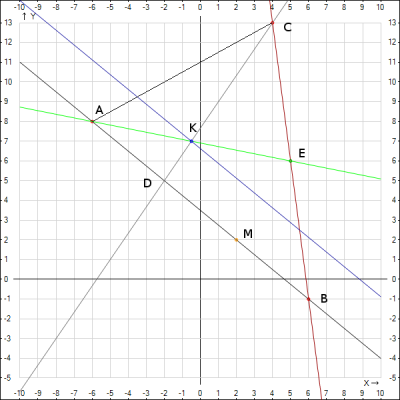
9. Нанесем точки и прямые на декартовую систему координат