Эта задача на нахождение локального максимума (экстремума) вида "найти наибольшую площадь (объем, длину и т.д.)".
Решение задачи сводится к нахождению функции (в данном случае площади) от одной переменной, а далее действуем по алгоритму нахождения экстремума.
Решаем.
Площадь прямоугольника равна $$S=a*b$$т.е. у нас две переменные. Нужно выразить одну переменную (сторону) через другую или найти общую для сторон переменную и выразить стороны через эту переменную.
Рассмотрим рисунок.
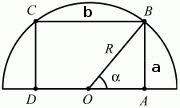
Рассмотрим прямоугольный треугольник ΔOAB. Стороны треугольника связаны между собой при помощи теоремы Пифагора и при помощи тригонометрических функций.
Рассмотрим первый способ - тригонометрический.
Будем считать, что R - радиус окружности - постоянная. Из треугольника ΔOAB можно найти его катеты (это стороны прямоугольника) \(a = AB = R\sin\alpha\), для второго катета (стороны) \(\frac{1}{2}b = R\cos\alpha => b = 2*R\cos\alpha\). Подставляем в формулу площади $$S=a*b = R\sin\alpha *2*R\cos\alpha = R^2\sin 2\alpha $$ Из рисунка видно, что угол принадлежит диапазону \(\alpha \in (0;90^0)\).
Получили функцию площади, зависящую от одной переменной - угла \(S(\alpha)\).
Теперь ищем локальный максимум (экстремум). Для этого находим производную от функции \(S(\alpha)\) $$S' = (R^2\sin 2\alpha )' = 2R^2*\cos 2\alpha$$ Приравниваем производную к нулю $$2R^2*\cos 2\alpha = 0 => \cos 2\alpha = 0 => $$$$ 2\alpha = \frac{\pi}{2} +\pi n => \alpha = \frac{\pi}{4} +\frac{\pi n}{2} $$Как я уже писал угол \(\alpha \in (0;\frac{\pi}{2})\), поэтому остается одно решение \(\alpha = \frac{\pi}{4}\). Подставляем полученное значение в формулу сторон и площади и находим прямоугольник с наибольшей площадью $$a = R\sin\frac{\pi}{4} = \frac{\sqrt 2}{2}R$$$$b = 2R\cos\frac{\pi}{4} = \sqrt 2 R$$$$S = R^2\sin 2\frac{\pi}{4}= R^2$$
То, что это локальный максимум понятно из того, что мы получили \(\sin 2\frac{\pi}{4} = \sin \frac{\pi}{2} = 1\). Если мы возьмем углы справа и слева , то синус всегда будет меньше единицы, т.е. полученная площадь наибольшая.





