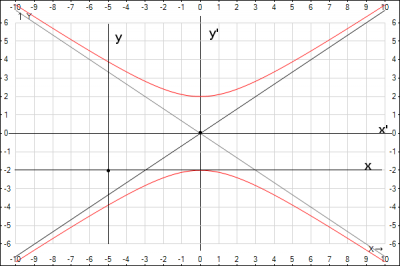
б) \(4х^2-9у^2-40х+36у+100=0\). Выделяем полный квадрат $$4(х^2-10x)- 9(у^2-4у)+100=0 => 4(х^2-2*5x+25-25)- 9(у^2-2*2у+4-4)+100=0 =>$$$$4((x-5)^2-25)- 9((y-2)^2-4)+100=0 => 4(x-5)^2-100- 9(y-2)^2+36+100=0 =>$$$$4(x-5)^2- 9(y-2)^2=-36 =>$$Разделим обе части уравнения на 36, получим $$\frac{(x-5)^2}{9}- \frac{(y-2)^2}{4}=-1$$ Получили уравнение гиперболы с центром в т. (5;2) и действительной осью, параллельной оси Oy. Для получения канонического уравнения необходимо сделать параллельный перенос осей. Введем новую систему координат в точке (5;2), Для этого введем новые координаты \(x'=x-5; y'=y-2\), получаем каноническое уравнение гиперболы $$\frac{x'^2}{9}- \frac{y'^2}{4}=-1$$ Для удобства построения гипербола построим асимптоты $$y= \pm \frac{b}{a}x = \pm \frac{2}{3}x'$$