Дані точки: А(11; 1), В(1; 8;), С(4; 2). І.Скласти рівняння: 1) прямої АВ; 2) висоти трикутника АВС Seekland INFO Сообщество взаимопомощи студентов и школьников / Спільнота взаємодопомоги студентів і школярів.

0 Голосов

Posted Ноябрь 10, 2013 by Аня Литвиненко

Всего просмотров: 7891

Дані точки: А(11; 1), В(1; 8;), С(4; 2).
І.Скласти рівняння:
1) прямої АВ;
2) висоти трикутника АВС, що проходить через вершину В;
3)прямої, що проходить через точку С паралельно прямій АВ;
4)медіани DАВС, що проходить через точку С;
5)серединного перпендикуляра до сторони АС .
ІІ. Розв”язати задачі:
1)Знайти довжину висоти DАВС, проведеної з вершини С.
2)Знайти проекцію точки А на пряму ВС.
3) Знайти кут між прямою АВ та прямою 2x-3y=0.

Лучший ответ

0 Голосов

Posted Ноябрь 10, 2013 by Вячеслав Моргун

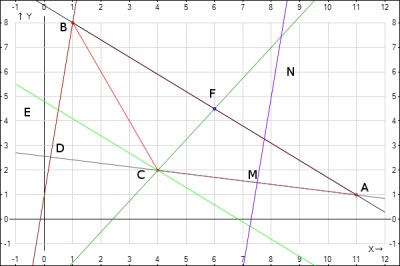
1. Составим уравнение прямой AB. Для этого воспользуемся уравнением прямой, проходящей через две заданные точки

$\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}$ подставляем координаты точек А(11; 1), В(1;8), получаем

$\frac{x-11}{1-11}=\frac{y-1}{8-1} =>y=-0,7x+8,7$
2. Составим уравнение высоты треугольника ΔABC, выходящую из вершины B. Назовем ее BD. Для этого найдем уравнение стороны AC и применим свойство угловых коэффициентов перпендикулярных прямых

$k_1=-\frac{1}{k_2}$ Уравнение прямой AC получим из формулы прямой, проходящей через две заданные точки А(11; 1), С(4; 2)

$\frac{x-11}{4-11}=\frac{y-1}{2-1} =>y=-\frac{1}{7}x+\frac{18}{7}$ Из этого уравнения получаем угловой коэффициент

$k_{AC}=-\frac{1}{7}$ .Тогда угловой коэффициент высоты BD будет равен

$k_{BD}=-\frac{1}{k_{AC}}=7$ . Для уравнение высоты BD у нас есть координаты одной точки В(1; 8) и угловой коэффициент

$k_{BD}=7$ получим уравнение высоты, воспользовавшись формулой прямой, проходящей через заданную точку в заданном направлении

$y-y_0=k(x-x_0)$ Подставляем полученные данные и получаем уравнение высоты BD

$y-8=7(x-1) =>y=7x+1$

3. Составить уравнение прямой, проходящей через точку C параллельно прямой AB. Назовем ее CE. Две прямые параллельны, значит их угловые коэффициенты равны. Уравнение прямой AB известно $y=-0,7x+8,7$ , тогда угловой коэффициент $k_{AB}=k_{CE}=-0.7$ . Угловой коэффициент нашли, координаты точки С(4; 2) известны, подставляем в уравнение прямой, проходящей через заданную точку в заданном направлении, получаем уравнение прямой, проходящей через точку C, параллельно прямой AB

$y-2=-0.7(x-4)=>y=-0,7x+4,8$
4. Медиана треугольника ΔABC, проходящую через точку C. Назовем ее CF. Медиана в точке F делит сторону AC пополам. Известны координаты точек А(11; 1) и В(1; 8), найдем координаты точки

$F(\frac{x_A+x_B}{2};\frac{y_A+y_B}{2}) =>F(\frac{11+1}{2};\frac{1+8}{2}) =>F(6;4.5)$ , тогда воспользуемся уравнением прямой, проходящей через две заданные точки С(4; 2) и F(6;4,5) и получим уравнение медианы CF

$\frac{x-4}{6-4}=\frac{y-2}{4,5-2} =>y=1,25x-3$
5. Составить уравнение серединного перпендикуляра к стороне AC. Назовем серединный перпендикуляр (медиатриса) MN. Серединный перпендикуляр - перпендикуляр проведенный к середине отрезка AC - точка M, найдем ее координаты при известных координатах точек А(11; 1), С(4; 2)

$M(\frac{11+4}{2};\frac{1+2}{2}) =>M(7,5;1,5)$ . Уравнение высоты BD на сторону AC известно

$y=7x+1$ . Серединный перпендикуляр также перпендикулярен AC, т.е. он параллелен BD, т.е. их угловые коэффициенты равны

$k_{AC}=k_{MN}=7$ . Воспользуемся уравнением прямой, проходящей через заданную точку M(7,5;1,5) в заданном направлении

$k_{MN}=7$ и получим уравнение серединного перпендикуляра MN

$y-1,5=7(x-7,5) =>y=7x-51$

Нанесем полученные уравнения прямых на декартовую систему координат