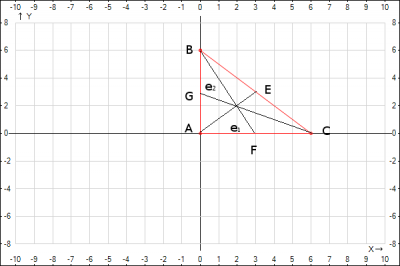
Согласно условия задачи векторы \(\vec{AB};\vec{AC}\) приняты за базисные. Введем обозначения \(\vec{AC}=e_1;\vec{AB}=e_2\). Векторы \(e_1;e_2\) являются базисом, значит они
1. линейно независимые
2. любой вектор плоскости можно разложить на базисные, т.е. можно представить в следующем виде \(\vec{a} = \alpha e_1 + \beta e_2\), т.е координаты вектора в базисе \((e_1;e_2)\) будет равны \(\vec{a}(\alpha;\beta)\)
Теперь понятно что искать.
1. Координаты вектора \(\vec{AE}\). По правилу треугольника получаем \(\vec{BC} = e_1-e_2\). Тогда \(\vec{AE}=e_2+\vec{BE} => \vec{AE}=e_2+\frac{1}{2}\vec{BC} =>\) подставляем формулу вектора BC и получаем \(\vec{AE}=e_2+\frac{1}{2}(e_1-e_2) => \vec{AE}=\frac{1}{2}e_1+\frac{1}{2}e_2\), т.е. координаты вектора равны \(\vec{AE}(\frac{1}{2};\frac{1}{2})\) в базисе \((e_1;e_2)\)
2. Координаты вектора \(\vec{BF}\). По правилу треугольника получим \(e_2+\vec{BF}=\frac{1}{2}e_1 =>\vec{BF}=\frac{1}{2}e_1-e_2\), т.е. координаты вектора равны \(\vec{BF}(\frac{1}{2};-1)\) в базисе \((e_1;e_2)\).
3. Координаты вектора \(\vec{CG}\). По правилу треугольника получим \(e_1+\vec{CG}=\frac{1}{2}e_2 =>\vec{CG}=-e_1 +\frac{1}{2}e_2\), т.е. координаты вектора равны \(\vec{CG}(-1;\frac{1}{2})\) в базисе \((e_1;e_2)\)