Чтобы установить какая это кривая проведем некоторые преобразования: $$x=2-\frac{1}{2}\sqrt{y^2-2y+5} => 2*(2-x)=\sqrt{y^2-2y+5} => $$возведем в квадрат обе части уравнения$$4*(2-x)^2=y^2-2y+5 =>$$Выделим полный квадрат по y $$4*(x-2)^2=y^2-2y+1-1+5 =>4*(x-2)^2=(y-1)^2+4 =>$$$$4*(x-2)^2-(y-1)^2=4 => (x-2)^2-\frac{(y-1)^2}{4}=1 $$Получили уравнение гиперболы в каноническом виде с центром в точке М(2;1), т.е. центр гиперболы не совпадает с началом координат, но оси симметрии параллельны осям координат и их уравнения x=2 и y=1. Из уравнения получим полуоси гиперболы: действительная полуось a = 1, мнимая полуось b =2. Зная полуоси найдем фокусное расстояние \(с = \sqrt{a^2+b^2}=\sqrt{1+4}=\sqrt{5}\). Т.к. действительная полуось лежит на прямой, параллельной оси Ox, то координаты фокусов находятся \(F_1(2-c;1);F_1(2+c;1)\) => \(F_1(2-\sqrt 5;1);F_1(2+\sqrt 5;1)\). Для удобства построения гиперболы построим асимптоты. Уравнение асимптот с учетом сдвига центра гиперболы рассчитывается по следующей формуле $$y-y_0=\pm \frac{b}{a}(x-x_0)$$где \((x_0;y_0)\) - точка M(2;1) - центр гиперболы. Подставляем известные данные и получаем $$y-1=\pm \frac{2}{1}(x-2) => y=\pm 2(x-2)+1$$Получили две асимптоты y = 2x-3 и y = -2x+5.
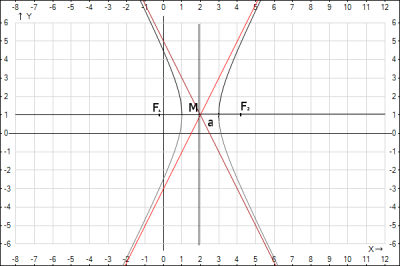
Нанесем на координатную плоскость и получим рисунок: