a) Длина стороны AB.
В задании известны координаты верши, поэтому длину стороны AB будем находить по формуле $$S=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$$Подставляем координаты вершин A(-2,4), B(3,1) и получаем длину стороны $$AB=\sqrt{(3+2)^2+(1-4)^2}=\sqrt{25+9}=\sqrt{34}$$
б) внутренний угол A в радианах
Внутренний угол будем искать как угол между прямыми AC и AB. Для этого составим уравнение этих прямых. У нас известны координаты вершин, поэтому применим формулу уравнения прямой, проходящей через две заданные точки $$\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}$$Подставляем координаты вершин и получаем
Уравнение прямой AB: $$\frac{x+2}{3+2}=\frac{y-4}{1-4} =>y=-\frac{3}{5}x+\frac{14}{5}$$
Уравнение прямой AC: $$\frac{x+2}{10+2}=\frac{y-4}{7-4} =>y=\frac{1}{4}x+\frac{9}{2}$$
Уравнение прямой BC: $$\frac{x-3}{10-3}=\frac{y-1}{7-1} =>y=\frac{6}{7}x-\frac{11}{7}$$
Внутренний угол A будем искать как угол между прямыми AB \(y=-\frac{3}{5}x+\frac{14}{5}\) и AC \(y=\frac{1}{4}x+\frac{9}{2}\) по формуле $$tg \alpha = |\frac{k_2-k_1}{1+k_2*k_1}|$$Подставим в формулу значения угловых коэффициентов прямых \(k_{AB}=-\frac{3}{5}\) и \(k_{AC}=\frac{1}{4}\) получим $$tg \alpha = |\frac{-\frac{3}{5}-\frac{1}{4}}{1-\frac{3}{5}*\frac{1}{4}}| = 1 => \alpha = \frac{\pi}{4}$$Эта формула дает нам угол между прямыми, который может быть острым или тупым, т.е. искомый угол может быть \( \alpha = \frac{\pi}{4}\) или \(\alpha = \pi -\frac{\pi}{4}\). Для того, чтобы определиться с углом, смотрим на рисунок, и видим, что в треугольнике угол A - острый, т.е. искомый угол равен $$\alpha = \frac{\pi}{4}$$
в) уравнение высоты CH и ее длину:
Для уравнения высоты CH у нас известны координаты вершины C(10;7), а также известно уравнение прямой AB, которая перпендикулярна высоте. Применим свойство угловых коэффициентов перпендикулярных прямых \(k_1=-\frac{1}{k_2}\). Угловой коэффициент прямой AB известен, он равен \(k_{AB}=-\frac{3}{5}\), тогда угловой коэффициент высоты CH равен \(k_{CH}=-\frac{1}{k_{AB}}=\frac{5}{3}\). Подставляем координаты вершины и угловой коэффициент в уравнение прямой, проходящей через заданную точку в заданном направлении $$y-y_0=k(x-x_0)$$и получаем $$y-7=\frac{5}{3}(x-10) =>y = \frac{5}{3}x-\frac{29}{3}$$
Длину высоты CH можно найти как расстояние от точки до прямой по формуле $$s=\frac{Ax_0+By_0+C}{\sqrt{A^2+B^2}}$$ подставляем в уравнение прямой AB \(y=-\frac{3}{5}x+\frac{14}{5} =>5y+3x-14=0\) координаты точки C и получаем $$CH=\frac{5*7+3*10-14}{ \sqrt{3^2+5^2}}=\frac{51}{ \sqrt{34}} \approx 8.7$$
г) уравнение медианы AM:
Для уравнения медианы известна координата точки A, а координаты точки M легко можно найти как полусумма координат точек B(3;1) и C(10;7). Получим координаты точки \(M(\frac{x_B+x_C}{2};\frac{y_B+y_C}{2}) => M(\frac{3+10}{2};\frac{1+7}{2}) => M(6,5;4)\). Зная две координаты точек A(-2;4) и M(6,5;4) получим уравнение медианы, как уравнение прямой, проходящей через две заданные точки $$\frac{x+2}{6.5+2}=\frac{y-4}{4-4}$$ В знаменателе y получили 0. Это значит, что при любом x значение y будет постоянным, т.е. медиана параллельна оси Ox. Уравнение медианы будет \(y=4\). Это хорошо видно из координат точек A(-2;4) и M(6,5;4), у которых координата y=4
д) точка пересечения медианы AM и высоты CH:
Для нахождения точки пересечения двух прямых составим систему уравнений, состоящую из уравнений этих прямых $$\begin{cases}y = 4\\y = \frac{5}{3}x-\frac{29}{3}\end{cases}=>\begin{cases}y = 4\\3y = 5x-29\end{cases}=> $$$$ \begin{cases}y = 4\\12 = 5x-29\end{cases}=>\begin{cases}y = 4\\ x=\frac{41}{5}=8.2\end{cases}$$Точка пересечения N имеет следующие координаты N(8.2;4)
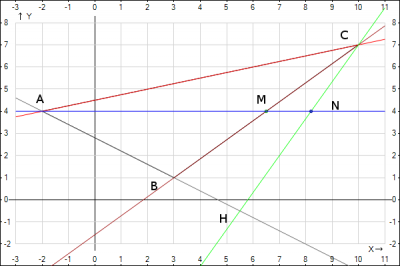
е) нарисовать рисунок треугольника ABC в декартовой системе координат.