Найдем стационарные (критические) точки (экстремумы и точки перегиба) и классифицируем их. Каждая стационарная точка - точка возможного экстремума. Для этого найдем первую производную и приравняем ее к 0, это и будут критические точки $$y'=(x^3-3x)' = 3x^2-3$$Приравниваем первую производную к нулю $$3x^2-3=0 =>x= \pm 1$$Получили две критические точки. Достаточным условием существования экстремума является изменение знака первой производной при переходе через критическую точку. Найдем значение первой производной справа и слева от критических точке и посмотрим на изменение знака производной при переходе через критическую точку
\(y'(-2)=3(-2)^2-3=9 > 0\)
\(y'(0)=3(0)^2-3=-3 < 0\)
\(y'(2)=3(2)^2-3=9 > 0\)
Теперь смотрим на изменение знака при переходе через критическую точку
1. x=-1, y'(-2) > 0 , y'(-1)=0, y'(0) < 0, т.е. получили + 0 - , т.е. функция имеет в этой точке локальный максимум.
2. x=1, y'(0) < 0 , y'(1)=0, y'(2) > 0, т.е. получили - 0 + , т.е. функция имеет в этой точке локальный минимум.
Мы получили, что обе критические точки являются экстремумами - точкой максимума и минимума.
Найдем интервалы выпуклости - вогнутости функции и точки перегибы: необходимым условием существования точки перегиба является равенство второй производной нулю y'' = 0. $$y''=(3x^2-3)'=6x$$$$6x=0=> x=0$$Достаточным условием существования точки перегиба является изменение знака второй производной при переходе через эту точку. Найдем значение второй производной справа и слева от этой точки
\(y''(-1)=6(-1)=-6 < 0\)
\(y''(1)=6*1=6 > 0\)
Получили, что слева от этой точки на интервале \((-\infty;0)\) - график имеет выпуклость вверх т.к. вторая производная y'' < 0 (выпуклая), а справа от точки на интервале \((0;\infty)\) - график имеет выпуклостью вниз т.к. вторая производная y'' > 0 (вогнутая).
Вывод: график функции \(y=x^3-3x\) имеет:
два экстремума в точках
x=-1 - локальный максимум
x=1 - локальный минимум,
точку перегиба
x=0 - точка перегиба.
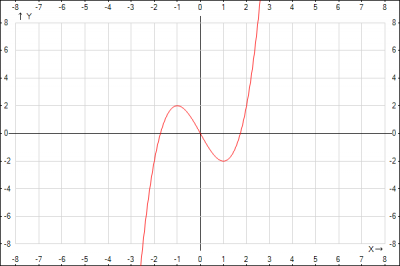
Построим график и проверим наши выводы.