1. Постройте график функции \(y= 3-3log_3x\).
Алгоритм построения графика \(y= 3-3log_3x\).
Строим график простейшей логарифмической функции при основании логарифма 3 \(y= log_3x\) (на рисунке красная кривая в точку)
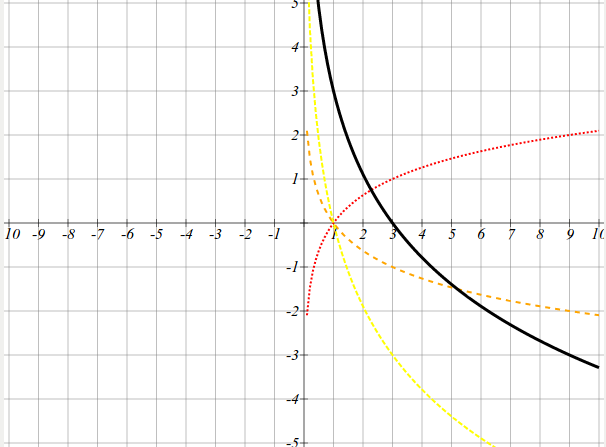
- Строим график функции \(y= -log_3x\) он получается путем зеркального отображения графика \(y= log_3x\) относительно оси х (на рисунке оранжевая кривая)
- Строим график функции \(y= -3log_3x\) он получается из графика функции \(y= -log_3x\) он получается следующим образом, при одинаковых значениях \(x\) значение \(y\) у графика функции \(y= -3log_3x\) будет в 3 раза больше, чем у \(y= -log_3x\) (на рисунке желтая кривая)
- Строим график функции \(y=3 -3log_3x\) он получается из графика функции \(y= -3log_3x\) путем параллельного переноса графика функции \(y= -3log_3x\) в верх вдоль оси \(y\) на 3 единицы (на рисунке черная кривая).
2. Найдите, на каком промежутке функция принимает наибольшее значение, равное 3 , и наименьшее значение , равное -3.
Как известно, функция \(log\) - монотонная функция, поэтому наибольшее и наименьшее значение она будет принимать только на концах промежутка, т.к. в данном случае функция убывающая (большему \(x\) соответствует меньший \(y\), то наибольшее значение будет началом интервала. а наименьшее значение будет концом интервала.
Найдем наибольшее значение 3 $$y= 3-3log_3x=3 => -3log_3x=0 =>log_3x=0 => x=1$$ смотрим на рисунок
Найдем наибольшее значение -3 $$y= 3-3log_3x=-3 => -3log_3x=-6 =>log_3x=2 => x=9$$ смотрим на рисунок
Т.о. получился интервал [1 ; 9]
3. Найдите, при каких значениях аргумента х значение функции больше 0.
Решим следующее уравнение $$y= 3-3log_3x >0 => 3log_3x log_3x < 1 => x < 3 => x\in (0; 3)$$смотрим на рисунок



