1.Уравнение стороны ВС
Т.к. у нас известны координаты двух точек B и C, уравнение стороны BC получим из уравнения прямой, проходящей через две заданные точки: $$\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}$$ Подставляем координаты точек и получаем $$\frac{x+4}{-1+4}=\frac{y-6}{2-6} => y = -\frac{4}{3}x+\frac{2}{3}$$ Уравнение прямой BC \( y = -\frac{4}{3}x+\frac{2}{3}\)
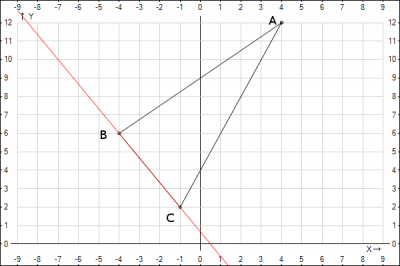
2.Уравнение высоты АК и ее длину.
Эта высота проходит через точку A и перпендикулярна прямой BC. Т.е. от прямой BC мы получим угловой коэффициент, воспользовавшись свойством перпендикулярных прямых \(k_1=-\frac{1}{k_2}\). Поставляем и находим $$k_{AK} = -\frac{1}{-\frac{4}{3}} =\frac{3}{4}$$У нас есть угловой коэффициент прямой и точка, через которую проходит эта прямая. Для получения уравнения прямой используем формулу прямой, проходящей через заданную точку в заданном направлении $$y-y_0=k(x-x_0)$$Подставляем известные данные и получим уравнение прямой AK $$y-12=\frac{3}{4}(x-4) =>y = \frac{3}{4}x+11$$ Уравнение прямой AK \(y = \frac{3}{4}x+9\)
Длина высоты - расстояние от точки до прямой. найдем расстояние, используя формулу $$d = \frac{Ax_0+By_0+C}{\sqrt{A^2+B^2}}$$Приведем уравнение прямой BC к общему виду $$ y = -\frac{4}{3}x+\frac{2}{3} =>4x+3y-2=0$$ где \(A=4; B=3\) - коэффициенты при переменных в уравнении прямой. Координаты точки известны, подставляем в уравнение расстояния $$d= \frac{4*4+3*12-2}{\sqrt{16+9}} = \frac{50}{5}=10$$Длина высоты \(AK=10\)
Из рисунка видно, что треугольник ABC прямоугольный.
3.Уравнение медианы СМ.
Медиана - прямая, проходящая через точку C и середину стороны AB. Найдем середину стороны AB и по двум известным координатам получим уравнение медианы CM. Найдем середину стороны AB - т. \(M(\frac{x_1+x_2}{2};\frac{y_1+y_2}{2})\) => \(M(\frac{4-4}{2};\frac{12+6}{2})\) => \(M(0;9)\). Получили две известные точки, через которые проходит медиана. Уравнение медианы $$\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1} =>$$подставляем координаты точек $$\frac{x+1}{0+1}=\frac{y-2}{9-2} =>y = 7x+9$$ Уравнение медианы CM \(y = 7x+9\).
4.Площадь этого треугольника.
Площадь треугольника равна \(S=\frac{1}{2}h*a\), где h - высота, она уже была получена \(AK=h=10\). Осталось найти длину \(BC=a\). Длину BC будем искать по формуле расстояния между двумя точками на плоскости $$d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$$Подставляем координаты точек B и C $$BC = \sqrt{(-4+1)^2+(6-2)^2} =5$$подставляем в формулу площади $$S_{ABC} = \frac{1}{2}*10*5=25$$



