В данном уравнении мы видим сумму членов второго порядка, но коэффициент при y отличен от 1 т.е. это эллипс. Каноническое уравнение эллипса $$\frac{x^2}{a^2}+\frac{y^2}{b^2} = 1$$ Приведем наше уравнение к каноническому, разделив все члены на 4, получаем $$х^2+2у^2-4=0 => \frac{x^2}{4}+\frac{y^2}{2} = 1$$
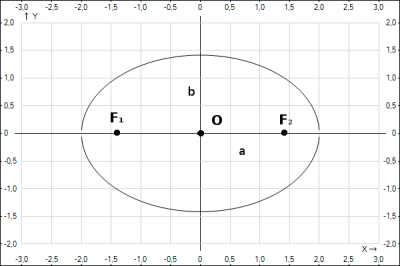
Получили эллипс:
1. с центром в начале координат O(0;0)
2. большая полуось \(a=2\), малая полуось \(b=\sqrt 2\)
3. фокальное расстояние \(c = \sqrt{a^2-b^2} =>c=\sqrt{4-2} => c=\sqrt 2\), тогда координаты фокусов эллипса будут \(F_1(-\sqrt 2;0),F_2(\sqrt 2;0)\)
4.Эксцентриситет \(\epsilon = \frac{c}{b} = \frac{c}{b} = \frac{\sqrt 2}{\sqrt 2} =1\)