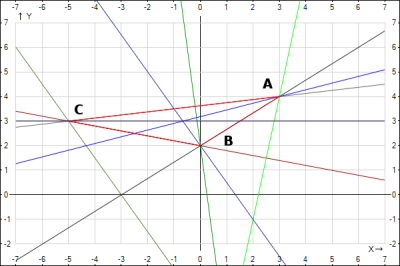
Для трех точек A(3;4), B(0;2), C(-5;3) проверяем
1. Образуют ли они треугольник.
Есть только один случай, когда три точки не образуют треугольник - когда они лежат на одной прямой, тогда треугольник вытягивается в отрезок. Проверку можно сделать графическим путем (нанести точки на координатную плоскость и соединить их отрезками) или проверить, лежат ли эти точки на одной прямой. Для этой проверки составим уравнение прямой проходящей через, например точки A и B и проверим лежит ли точка C на этой прямой.
Воспользуемся уравнением прямой, проходящей через две заданные точки $$\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1} \quad (1)$$ Подставляем координаты точек A(3;4), B(0;2), получаем $$\frac{x-3}{0-3}=\frac{y-4}{2-4}=>\frac{x-3}{3}=\frac{y-4}{2} =>y = \frac{2}{3}x+2$$ Теперь осталось только подставить координаты третьей точки в это уравнение, получаем \(3 = \frac{2}{3}(-5)+2 =>3 = -\frac{4}{3}\) получили ложное равенство, т.е. через точку C(-5;3) прямая не проходит.
2. Записать уравнения сторон треугольника.
Уравнение стороны AB было получено в п.1 $$y = \frac{2}{3}x+2$$
Уравнение стороны AC получим аналогично $$\frac{x-3}{-5-3}=\frac{y-4}{3-4} =>y = \frac{1}{8}x+\frac{29}{8}$$
Для стороны BC $$\frac{x-0}{-5-0}=\frac{y-2}{3-2} =>y = -\frac{1}{5}x + 2$$
3. Уравнения высот треугольника.
В задаче известны координаты вершин, а в п.2 получили уравнения сторон треугольника. Высоты будут проходить через вершину треугольника перпендикулярно противолежащей к этой вершине стороне. Известно свойство перпендикулярных прямых $$k_1*k_2=-1$$ где \(k_1,k_2\) - угловые коэффициенты прямых.
Найдем уравнение высоты, опущенной из вершины A(3;4). Для этого воспользуемся уравнением прямой, проходящей через заданную точку в заданным направлением. Направление прямой задается ее угловым коэффициентом \(k\) $$y-y_0=k(x-x_0) \quad (2)$$ Т.к. эта высота перпендикулярна прямой BC ее угловой коэффициент равен \(k_{A}=-\frac{1}{k_{BC}}\) Из п.2 видим, что \(k_{BC} = -\frac{1}{5}\)=> \(k_{A}=5\). Подставляем координаты точки A(3;4) и значение углового коэффициента в уравнение прямой и получаем $$y-4 = -5(x+3) =>y = 5x-11$$
Найдем уравнение высоты, опущенной из вершины B(0;2).
Высота будет перпендикулярна прямой AC, тогда угловой коэффициент будет равен \(k_{B}= -8\). Запишем уравнение прямой $$y - 2 = -8(x-0) =>y = -8x+2$$
Найдем уравнение высоты, опущенной из вершины C(-5;3).
Высота будет перпендикулярна прямой AB, тогда угловой коэффициент будет равен \(k_{C}= -\frac{3}{2}\). Запишем уравнение прямой $$y - 3 = -\frac{3}{2}(x+5) =>y = -\frac{3}{2}x-\frac{9}{2}$$
4. Уравнения медиан треугольника.
Медиана проходит через вершину треугольника и середину противолежащей этой вершине сторону . Координаты середины между вершинами рассчитываются как \(\frac{x_1+x_2}{2};\frac{y_1+y_2}{2}\). Т.о. у нас есть две точки через которые проходит прямая, т.е. воспользуемся уравнением прямой, проходящей через две точки.
Найдем медиану из вершины A(3;4). Серединой между вершинами BC будет точка с координатами \(M_{BC}(\frac{0-5}{2};\frac{2+3}{2}) =>M_{BC}(-\frac{5}{2};\frac{5}{2})\). Подставляем координаты точек в уравнение прямой (1),получаем $$\frac{x-3}{-\frac{5}{2}-3}=\frac{y-4}{\frac{5}{2}-4} =>y = \frac{3}{11}x+\frac{35}{11}$$
Найдем медиану из вершины B(0;2). Серединой между вершинами AC будет точка с координатами \(M_{AC}(\frac{3-5}{2};\frac{4+3}{2}) =>M_{AC}(-1;\frac{7}{2})\). Подставляем координаты точек в уравнение прямой (1),получаем $$\frac{x-0}{-1-0}=\frac{y-2}{\frac{7}{2}-2} =>y = -\frac{2}{3}x+2$$
Найдем медиану из вершины C(-5;3). Серединой между вершинами AB будет точка с координатами \(M_{AB}(\frac{3+0}{2};\frac{4+2}{2}) =>M_{AB}(\frac{3}{2};3)\). Подставляем координаты точек в уравнение прямой (1),получаем $$\frac{x+5}{\frac{3}{2}+5}=\frac{y-3}{3-3} =>y = 3$$Получили знаменатель при y равный 0, т.е. прямая параллельная оси \(Ox\) и проходит через точку C(-5;3)
5. Найти площадь треугольника. Площадь треугольника равна $$S=\frac{1}{2}ah$$ где \(a\) - длина стороны, а \(h\) - высота, опущенная на эту сторону. Рассмотрим высоту из вершины \(B\) и сторону AC. Длину стороны AС находим по формуле длины отрезка $$a = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$$Подставляем координаты вершин и получаем $$AC = \sqrt{(-5-3)^2+(3-4)^2} = \sqrt{64+1} = \sqrt{65}$$ Найдем координаты точки пересечения высоты из вершины B и прямой AC $$\begin{cases}y = \frac{1}{8}x+\frac{29}{8}\\y = -8x+2\end{cases}=>\begin{cases} \frac{1}{8}x+\frac{29}{8} = -8x+2\\ y = -8x+2\end{cases}=>\begin{cases}x =- \frac{1}{5}\\ y = \frac{18}{5}\end{cases}$$ Зная две координаты, найдем длину высоты $$h = \sqrt{(-\frac{1}{5}-0)^2+(\frac{18}{5}-2)^2} = \sqrt{\frac{13}{5}}$$ Находим площадь, подставляем полученные длины стороны и высоты $$S = \frac{1}{2}AC*h= \frac{1}{2}\sqrt{65}*\sqrt{\frac{13}{5}} = \frac{13}{2}$$
6. Найти угол A. Длина одного катета была получена в п. 5 \(h = \sqrt{\frac{13}{5}}\). Найдем длину отрезка \(AB=\sqrt{(0-3)^2+(2-4)^2} =\sqrt{9+4}=\sqrt{13}\), тогда угол будет равен $$\sin A = \frac{h}{AB} = \frac{\sqrt{\frac{13}{5}}}{\sqrt{13}} = \frac{1}{\sqrt{5}}$$ Угол будет равен $$A = \arcsin \frac{1}{\sqrt 5}$$
Все прямые нанесены на рисунок.
Красные линии - треугольник
Зеленые - высоты.
Синие - медианы.
Синие - медианы.