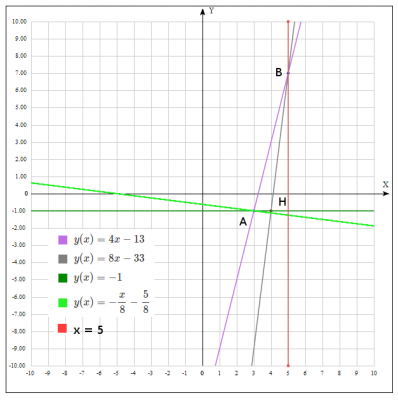
Дано две вершини трикутника А(3; -1), B(5; 7) та точка Н(4; -1) перетин его висот.
Записати рівняння сторін цього трикутника.
Знайдемо рівняння сторони \(AB)\
1. Рівняння прямої AB
В завданні дано координати двох вершин. Отримаємо рівняння сторони, використовуючи формулу рівняння прямої, що проходить через дві задані точки $$ \frac{x-x_1}{x_2-x_1} = \frac{y-y_1}{y_2-y_1} $$ Підставляємо координати вершин А(3 ; -1), B(5; 7) в рівняння і отримуємо $$ \frac{x-3}{5-3} = \frac{y + 1}{7 + 1} = > y = 4x - 13 $$
Для того, щоб знайти рівняння решти сторін,
знайдемо рівняння висот:
2. що проходить через вершину A і перпендикулярну BC , назвемо її AH. Дві точки у нас відомі, застосуємо рівняння прямої що проходить через дві задані точки А(3; -1), Н(4; -1) $$ \frac{x-3}{4-3} = \frac{y + 1}{- 1 + 1} $$ Оскільки в знаменнику \(у \) - \(-1+1 = 0\), означає що пряма паралельна осі Ox і її рівняння \(y = -1 \)
3. що проходить через вершину B і перпендикулярну AC , назвемо її BH. Дві точки у нас відомі, застосуємо рівняння прямої що проходить через дві задані точки В(5; 7), Н(4; -1) $$ \frac{x-5}{4-5} = \frac{y-7}{- 1-7} = > y = 8x-33 $$
Мета пошуку рівнянь висот наступна: як відомо, кутові коефіцієнти перпендикулярних прямих пов'язані наступним співвідношенням \(k_1 = - \frac{1}{k_2} \), тобто для рівнянь двох, що залишилися, сторін у нас є по одній вершині і кутові коефіцієнти.
Отримаємо ці рівняння:
4. Рівняння прямої AC . Для цього рівняння у нас є координати вершини А(3; -1). Знайдемо кутовий коефіцієнт, знаючи кутовий коефіцієнт перпендикулярної прямої BH, який дорівнює \(k_{BH} = 8 \) = > \(k_{ AC} = - \frac{1}{k_{BH}} = - \frac{1}{8} \). Тоді рівняння прямої AC дорівнює $$ y + 1 = - \frac{1}{8}(x-3) = > y = - \frac{1}{8} x - \frac{5}{8} $$
5. Рівняння прямої BC. Відомо, що висота AH перпендикулярна цій стороні паралельна осі Ox, значить ця сторона буде паралельна осі Oy і при цьому проходити через вершину В(5; 7), тобто її рівняння буде \(x = 5 \)
Рівняння трьох прямих сторін трикутника знайдені. Постоїмо трикутник