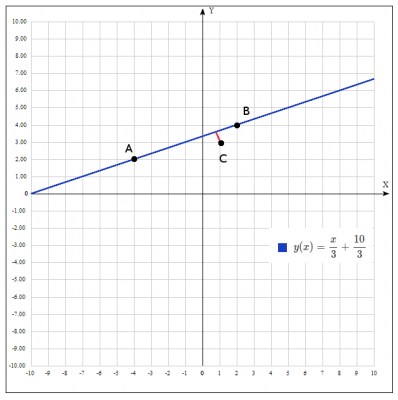
Даны вершины треугольника АВС: A(-4;2), B(2;4), C(1,3)
Составить уравнение AB. Найти длину высоты CH.
1. Составить уравнение AB.
Уравнения стороны будем искать при помощи формулы уравнения прямой, проходящей через две заданные точки \( \frac{x-x_1}{x_2-x_1} = \frac{y-y_1}{y_2-y_1} \quad (1) \) Подставляем координаты вершин:
уравнение стороны \(AB\), при известных координатах вершины \(A(-4;2), B(2;4)\) $$ AB \quad \frac{x+4}{2+4} = \frac{y-2}{4-2} => y = \frac{x}{3} +\frac{10}{3}$$
Ответ: уравнение стороны \(AB\): \(y = \frac{x}{3} +\frac{10}{3}\)
Длина высоты \(CH\), опущенной из вершины \(C\) на сторону \(AB\).
Длину высоту CH будем искать как расстояние от точки C до прямой AB по формуле $$ d = \frac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}} \quad (2)$$ где \((x_0;y_0)\) - координаты точки, а \(Ax_0+By_0+C =0\) - общее уравнение прямой, расстояние до которой ищется.
Приводим уравнение прямой \(AB\) к общему виду \( y = \frac{x}{3} +\frac{10}{3} =>-x+ 3y -10 = 0\), где \(A =-1\), \(B = 3\), координаты точки C(1,3) => \(x_0=1;y_0=3\) подставляем в формулу (2) $$ d = \frac{|-1+ 3*3 -10 |}{\sqrt{(-1)^2+3^2}} = \sqrt{\frac{2}{5}} \approx 0,62$$
Ответ: длина высоты CH равна \(d \approx 0,62\).