Решение: найдем площадь фигуры, ограниченную линиями \( y= 2- x^2 \quad y = x \)
Строим кривые:
1. \( y= 2- x^2 \) - парабола.
Проанализируем уравнение параболы. Знак минус перед \(x^2\) указывает на то, что оси параболы направлены вниз. Вершина параболы находится в точке B(0;2).
2. \(y = x \) - уравнение прямой, проходящей через начало координат. Прямая расположена в первой и третьей четверти.
Строим рисунок:
Нужно найти площадь криволинейной фигуры \(ABC\)
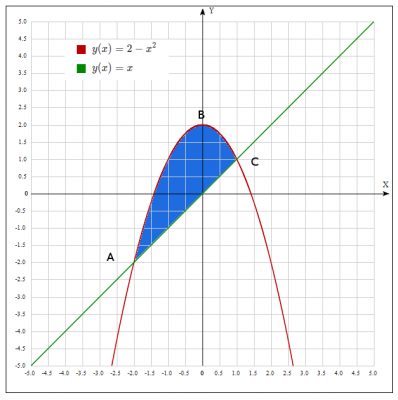
Вспомним геометрический смысл определенного интеграла: если фигура ограниченна кривыми \(y_1=g(x)\) и \(y_2=f(x)\), причем функция \(f(x) > g(x)\), то определенный интеграл \(S = \int_a^b[f(x) - g(x)]dx\) равен площади фигуры этой фигуры.
Согласно условия задачи \( y_2 = 2- x^2; \quad y_1 = x \), тогда искомая площадь фигуры \(ABC\) равна $$S_{ABC} = \int_A^C(2- x^2 - x)dx $$ для нахождения интеграла нужно найти координаты \(x\) точек A и C. Это точки пересечения кривых, поэтому решим систему уравнений $$\begin{cases} y = 2- x^2 \\ y = x \end{cases} => \begin{cases} x^2 + x - 2=0 \\ y = x \end{cases} => \begin{cases} x_1 = -2;x_2=1 \\ y_1 = -2; y_2 = 1 \end{cases} $$ Подставляем координаты \(x\) точек в интеграл $$S_{ABC} = \int_{-2}^{1}(2- x^2 - x)dx =$$ Для нахождения определенного интеграла, применим формулу Ньютона-Лейбница \(\int_a^bf(x)dx = F(x)|_a^b = F(b) - F(a)\), получаем $$ = 2x - \frac{x^3}{3}- \frac{x^2}{2}|_{-2}^{1} = 2 - \frac{1}{3}- \frac{1}{2} + 4 - \frac{8}{3} + \frac{4}{2} = 4.5 $$
Ответ: площадь фигуры, которая ограничена линиями \( y= 2- x^2\quad y = x \) равна \(S_{ABC} = 4.5\)



