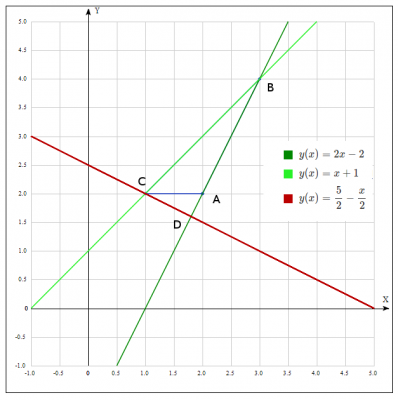
Задано координати вершин трикутника: А(2;2), В(3;4), С(1;2)
Знайти:
1) Рівняння сторони АВ
2) Внутрішній кут В
3) Рівняння і довжину висоти СD
4) Площу трикутника АВС
Розв’язання:
1) Рівняння сторони АВ
Рівняння сторони будемо шукати за допомогою формули рівняння прямої, що проходить через дві задані точки \( \frac{x-x_1}{x_2-x_1} = \frac{y-y_1}{y_2-y_1} \quad (1) \) Підставляємо координати вершин:
рівняння сторони \( AB \), при відомих координатах вершини \( А(2;2) В(3;4)\) $$ AB \quad \frac{x-2}{3-2} = \frac{y-2}{4-2} => y =2x - 2$$
Відповідь: рівняння сторони \(AB\): \( y =2x - 2 \quad (2)\)
2) Внутрішній кут \( \angle B\):
Кут \( \angle ABC \) - кут між прямими AB і BC - \( \angle ABC = \beta \) будемо шукати за формулою $$ tg \beta = | \frac{k_2-k_1}{1 + k_1k_2} | \quad (3) $$
\(k_1, k_2 \) - кутові коефіцієнти прямих AB і BC.
Кутовий коефіцієнт прямої AB дорівнює \(k_ {AB} = 2 \).
Знайдемо кутовий коефіцієнт прямої BC. Рівняння прямої будемо шукати за допомогою формули рівняння прямої, що проходить через дві задані точки \( \frac{x-x_1}{x_2-x_1} = \frac{y-y_1}{y_2-y_1} \quad (1) \)
Підставляємо координати вершин В(3;4), С(1;2):
рівняння сторони BC , при відомих координатах вершини В(3;4), С(1;2) $$ BC \quad \frac{x - 3}{1 - 3} = \frac{y-4}{2-4} => \quad y = x + 1 $$
Відповідь: рівняння сторони \(BC\) дорівнює: \( \quad y = x + 1 \)
Кутовий коефіцієнт прямої \(k_ {BC} = 1 \), підставляємо в (3) $$ tg \beta = |\frac{ 2 - 1}{1+ 2*1 } | = \frac{1}{3} => \quad \beta = 18.43^0 $$
Відповідь : кут \( \angle \beta \) між прямими AB і BC дорівнює \( \angle \beta = 18.43^0 \)
3) Рівняння і довжину висоти CD
Висота CD опущена з вершини C на сторону AB, тобто з умови відома одна координата точки С(1;2) і напрям - пряма перпендикулярна прямий AB.
Скористаємося властивістю кутових коефіцієнтів перпендикулярних прямих: \(k_1 = - \frac{1}{k_2} \).
Знайдемо кутовий коефіцієнт прямої сторони CD з рівняння (2).
Отримали \(k_{AB} = 2 => \) \(k_{CD} = - \frac{1}{AB} = -\frac{1}{2} \). Знайдемо рівняння прямої CD, для цього скористаємося рівнянням прямої що проходить через задану точку С(1;2) в заданому напрямку \(k_{CD} = - \frac{1}{2} \) $$ y - y_0 = k (x - x_0) \quad (4) $$ отримаємо $$ y - 2 = -\frac{1}{2} (x - 1) => y = \frac{5}{2} - \frac{1}{2}x$$
Відповідь: рівняння висоти CD: \( y =\frac{5}{2} - \frac{1}{2}x\)
Довжина висоти CD
Довжину висоти CD будемо шукати як відстань від точки D до прямої AB за формулою $$ d = \frac{| Ax_0 + By_0 + C |}{\sqrt{A^2 + B^2}} \quad(5) $$ де \((x_0; y_0) \) - координати точки С(1;2), а
\(Ax_0 + By_0 + C = 0 \) - загальне рівняння прямої, відстань до якої шукається
$$y =2x - 2 => 2x - y - 2 = 0 => A = 2; \quad B = -1 $$ Підставляємо дані у формулу $$ d_{CD} = \frac{| 2*1 - 2 - 2 |}{\sqrt{2^2 + (-1)^2}} = \frac{2}{ \sqrt{5}} \approx 0.89 $$
Відповідь: довжина висоти CD: \(d_{CD} \approx 0.89 \)
4) Площу трикутника АВС
Площа трикутника будемо шукати за формулою \(S = \frac{1}{2}ah \). Довжина висоти вже відома див. П. 3) \(h = CD = \frac{2}{ \sqrt{5}} \). Необхідно знайти довжину сторони \(AB \) як відстань між точками А(2; 2), В(3; 4). Відстань між точками знаходиться за формулою Піфагора \(a = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2} \), одержуємо $$ a = \sqrt{(2-3)^2 + (2-4)^2} = \sqrt{5} $$ підставляємо в формулу площі трикутника $$ S_{ΔABC} = \frac{1}{2}ah = \frac{1}{2}\sqrt{5} \frac{2}{\sqrt{5}} = 1 $$
Відповідь: площа трикутника дорівнює \(S_ {ΔABC} = 1 \)