Все геометрические задачи начинаются с построения рисунка. Качественный рисунок - залог правильного решения задачи. Рассмотрим рисунок.
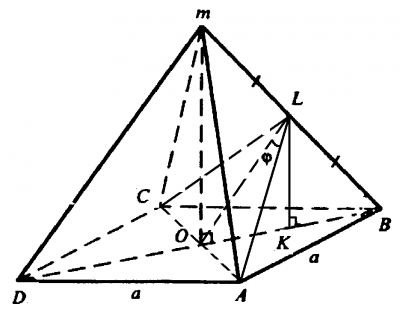
Правильная четырехугольная пирамида - пирамида в основании которой лежит правильный четырех угольник (квадрат), а вершина проецируется в его центр (точку пересечения диагоналей квадрата). Обозначим точкой \(O\) - центр квадрата (точка пересечения диагоналей). Т.о. в задаче необходимо найти \(MO\) - высота правильной пирамиды
Найдем угол между прямыми \(DM\) и \(AL\), этот угол равен \(\phi = 60^0\). Найдем плоскость в которых лежит одна из этих прямых и прямая параллельная другой прямой. Рассмотрим треугольник \(ΔDMB\). В этом треугольнике есть одна из прямых \(DM\) и точка \(L\), которая принадлежит прямой \(AL\). Проведем прямую , которая параллельна прямой \(DM\) и проходит через точку \(L\). Это будет прямая \(OL\) - средняя линия треугольника \(ΔDMB\), т.к. она проходит через середину \(MB\) и параллельна \(MD\), соответственно она разделит \(DB\) на две равные части, т.е. пройдет через точку \(O\) - центр квадрата. Тогда угол \(\angle{OLA} = \phi = 60^0\). Рассмотрим \(ΔOLA\). В этом треугольнике известен угол и можно найти сторону \(OA\), а из треугольника \(ACL\), который равнобедренный \(CL=AL\), т.к. все грани правильной пирамиды равны (\(ΔMCB = ΔMAB\)) следует, что \(LO\) - медиана, опущенная на основание равнобедренного треугольника, то она является и высотой и биссектрисой этого треугольника. Эти рассуждения нужны были, чтобы получить, что \(ΔOLA\) - прямоугольный треугольник. Тогда мы можем найти сторону $$OL = OA*\mbox{ctg}60^0$$ \(OA = \frac{1}{2}AC = AB \frac{\sqrt 2}{2} = a \frac{\sqrt 2}{2}\) => $$OL = a \frac{\sqrt 2}{2}*\mbox{ctg}60^0 = a \frac{\sqrt 2}{2}*\frac{1}{\sqrt 3} = 6*\frac{\sqrt 2}{2}*\frac{1}{\sqrt 3} = \sqrt 6$$помним, что гипотенуза квадрата - катет прямоугольного равнобедренного треугольника и по теореме Пифагора она равна \(AC = \sqrt{AB^2+BC^2} = \sqrt{a^2+a^2} = a\sqrt 2\), а точка \(O\) - делит диагонали пополам.
Опустим перпендикуляр из точки \(L\) на диагональ \(DB\) - \(KL\) - средняя линия треугольника \(ΔOMB\), т.е. отрезок \(OK = \frac{1}{2}OB = \frac{1}{2}OA = a \frac{\sqrt 2}{4} = 6* \frac{\sqrt 2}{4} = \frac{3}{\sqrt{2}}\). Воспользуемся свойством средней линии \(2KL = MO\). Найдем \(KL\) из прямоугольного треугольника \(ΔOLK\), в котором известна гипотенуза \(OL\) и катет \(OK\). По теореме Пифагора найдем \(LK = \sqrt{OL^2 - OK^2} = \sqrt{ (\sqrt 6)^2 - ( \frac{3}{\sqrt{2}})^2 } = \sqrt{6 - \frac{9}{2}} = \sqrt{\frac{3}{2}} => \) $$MO = 2KL = 2*\sqrt{\frac{3}{2}} = \sqrt 6$$Ответ: высота правильной четырехугольной пирамиды равна \(MO = \sqrt{6}\)



